1 0000 X 1 0000
vittoremobilya
Sep 12, 2025 · 6 min read
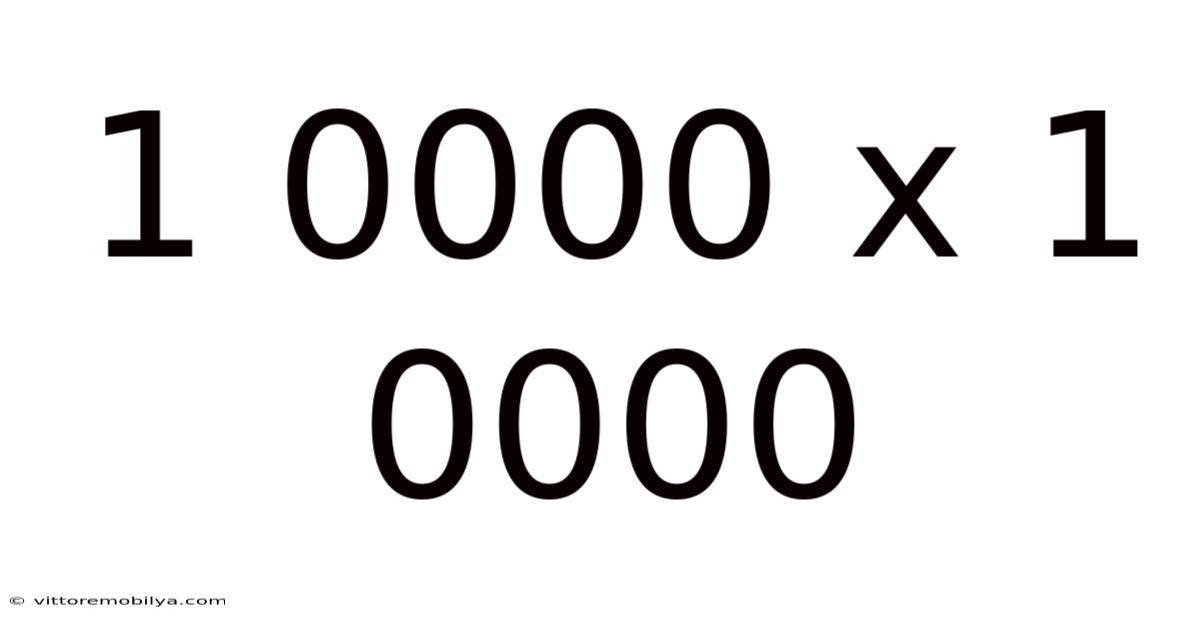
Table of Contents
Exploring the Immensity: A Deep Dive into 10,000 x 10,000
This article delves into the seemingly simple yet surprisingly profound calculation of 10,000 multiplied by 10,000. While the answer might seem straightforward, exploring the implications of this calculation opens doors to understanding large numbers, exponential growth, and the vast scales present in various fields like astronomy, finance, and computer science. We'll break down the calculation, examine its practical applications, and explore the conceptual significance of such a large number.
Understanding the Basics: Multiplication and Large Numbers
At its core, 10,000 x 10,000 is a straightforward multiplication problem. We're essentially asking: "What is the total if we have 10,000 groups, each containing 10,000 items?" The answer, obtained through simple multiplication, is 100,000,000 (one hundred million).
While the calculation itself is simple, the magnitude of the result is significant. One hundred million is a number that's difficult to truly grasp intuitively. We rarely encounter quantities of this size in our daily lives. To put it into perspective, consider:
- Population: The population of many medium-sized countries is in the tens of millions.
- Money: One hundred million dollars represents a substantial fortune.
- Distance: While not directly related to distance in a linear way, it represents a vast amount of data points or computational operations.
This highlights the importance of understanding not just the calculation but also the scale and implications of the resulting number.
Breaking Down the Calculation: Different Approaches
While simple multiplication provides the immediate answer, exploring different approaches helps deepen our understanding:
-
Standard Multiplication: The most straightforward method involves the traditional multiplication algorithm taught in elementary school. This involves multiplying each digit systematically, carrying over values as needed. For 10,000 x 10,000, this is relatively straightforward, but becomes more complex with larger numbers.
-
Scientific Notation: For extremely large numbers, scientific notation provides a more concise and manageable representation. 10,000 can be written as 10<sup>4</sup>. Therefore, 10,000 x 10,000 becomes 10<sup>4</sup> x 10<sup>4</sup>. Using the rules of exponents, we add the exponents: 10<sup>(4+4)</sup> = 10<sup>8</sup> = 100,000,000. This method is particularly useful when dealing with much larger numbers where standard multiplication becomes cumbersome.
-
Logarithms: Logarithms offer another powerful tool for working with large numbers. Taking the logarithm (base 10) of 10,000 gives us 4. Therefore, log(10,000 x 10,000) = log(10,000) + log(10,000) = 4 + 4 = 8. Taking the antilog (10<sup>8</sup>) gives us the answer: 100,000,000. This approach showcases the logarithmic properties of multiplication.
Understanding these different methods allows us to tackle increasingly larger numbers with greater efficiency and comprehension.
Practical Applications: Where Do We Encounter Such Numbers?
While 10,000 x 10,000 might seem abstract, numbers of this magnitude frequently appear in various real-world contexts:
-
Data Storage and Processing: In the digital world, 100 million represents a significant amount of data. Consider the number of pixels in a high-resolution image, the size of a large database, or the number of transactions processed by a financial institution in a given period. Understanding the scale helps in planning storage capacity, processing power, and network bandwidth.
-
Finance and Economics: In financial modeling, macroeconomic analysis, or portfolio management, dealing with millions or billions is commonplace. Calculations involving large populations, economic indicators, or investment strategies often involve numbers far exceeding 100 million.
-
Scientific Research: Many scientific fields deal with incredibly vast numbers. Astronomy, for instance, involves distances and quantities measured in astronomical units, light-years, and numbers of stars and galaxies far exceeding 100 million. Similarly, fields like genomics and molecular biology handle immense quantities of data related to DNA sequences and biological processes.
-
Computer Simulations: Complex computer simulations, such as climate modeling, weather forecasting, or fluid dynamics, require processing vast amounts of data and performing billions of calculations. The performance and efficiency of these simulations are critically dependent on handling such large numbers effectively.
The Conceptual Significance: Understanding Scale and Magnitude
The true significance of 10,000 x 10,000 extends beyond the numerical answer. It challenges us to grapple with the concept of scale and magnitude. Understanding the difference between one million, one hundred million, and one billion requires a nuanced appreciation for exponential growth. This understanding is crucial in various aspects of life, including:
-
Financial Literacy: Grasping large numbers is essential for making informed financial decisions, understanding investments, and planning for the future.
-
Scientific Reasoning: In science, the ability to interpret and comprehend data presented in various scales is vital for analyzing results and drawing meaningful conclusions.
-
Data Analysis: Effectively interpreting and visualizing large datasets requires a firm grasp of magnitude and scale, enabling us to identify trends, patterns, and anomalies.
-
Problem Solving: Many complex problems require the ability to think in terms of large-scale implications and consequences. This involves not only performing calculations but also making informed judgments about scale and impact.
Beyond 100 Million: Exploring Exponential Growth
The calculation of 10,000 x 10,000 provides a stepping stone to understanding exponential growth. If we continue this pattern, multiplying the result by 10,000 again, we quickly reach unimaginable numbers. This illustrates how exponential growth can lead to incredibly rapid increases in quantity over time. This concept is relevant to:
-
Population Growth: Understanding exponential growth is crucial for predicting population trends and managing resources accordingly.
-
Technological Advancements: Moore's Law, which describes the exponential growth in computing power, demonstrates the impact of exponential growth on technological advancement.
-
Compound Interest: The power of compound interest demonstrates how seemingly small increases can accumulate to substantial amounts over time due to exponential growth.
Frequently Asked Questions (FAQ)
-
What are some real-world examples of 100 million being used? The number 100 million can represent the approximate population of many countries, the annual budget of large corporations, the number of transactions processed by financial institutions daily, or the number of social media users on a popular platform.
-
How does this calculation relate to scientific notation? 10,000 can be expressed as 10<sup>4</sup>. Thus, 10,000 x 10,000 = 10<sup>4</sup> x 10<sup>4</sup> = 10<sup>8</sup> = 100,000,000. Scientific notation simplifies working with very large numbers.
-
What are some other ways to visualize 100 million? Consider stacking 100 million one-dollar bills—the height would be impressive! Or imagine a stadium filled 100 million times with people—a mind-boggling number indeed!
-
Is there a limit to how large numbers can get? No, there is no upper limit to the size of numbers. Numbers can theoretically continue to increase infinitely.
Conclusion: The Power of Understanding Scale
The calculation of 10,000 x 10,000, while seemingly simple, offers a gateway to understanding large numbers, exponential growth, and the vast scales encountered in various fields. The resulting 100 million isn't just a numerical answer; it's a concept that prompts us to grapple with magnitude, scale, and the implications of exponential growth. Appreciating the scale and significance of such numbers enhances our ability to make informed decisions, interpret data, and solve complex problems across diverse disciplines. It's a fundamental stepping stone to a deeper understanding of the quantitative world around us.
Latest Posts
Latest Posts
-
Prayer For Fasting And Prayer
Sep 12, 2025
-
Sona Masoori Rice Vs Basmati
Sep 12, 2025
-
Son Is Horny For Mom
Sep 12, 2025
-
Does Racetrac Have Free Air
Sep 12, 2025
-
What Smell Do Mice Hate
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1 0000 X 1 0000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.