1 3 Of 1 4
vittoremobilya
Sep 24, 2025 · 5 min read
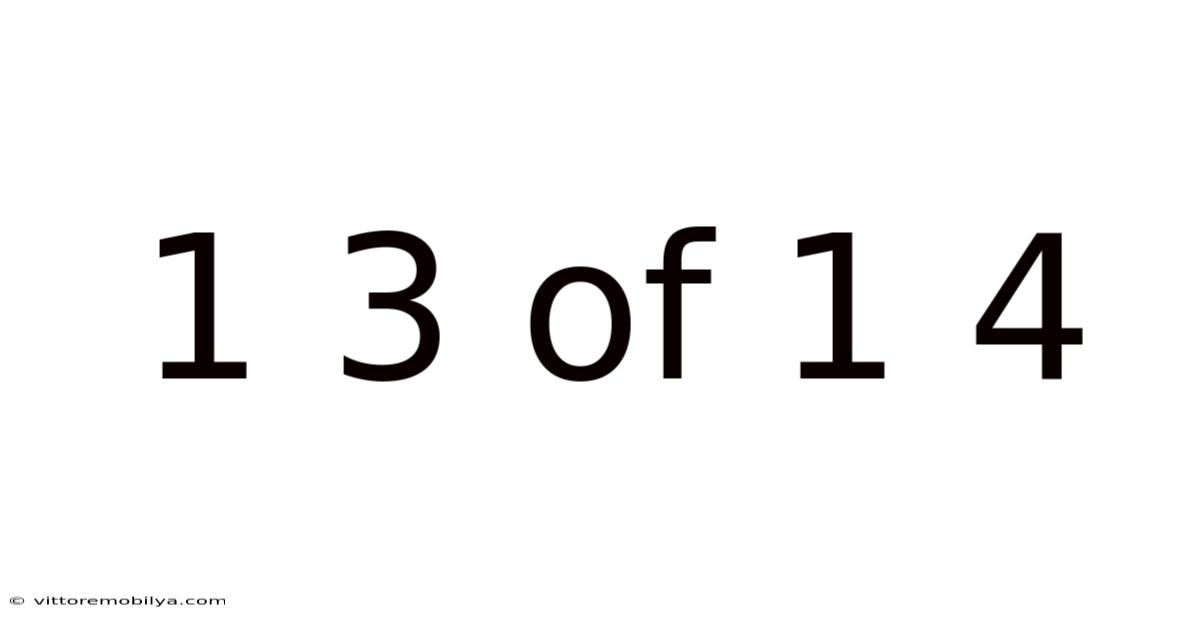
Table of Contents
Decoding the Fraction: Understanding 1 3/14
This article delves into the seemingly simple yet surprisingly multifaceted world of the fraction 1 3/14. We'll explore its meaning, various representations, practical applications, and even touch upon the mathematical concepts behind it. Understanding fractions like 1 3/14 is crucial for a solid foundation in mathematics and its application in various fields. This comprehensive guide will equip you with the knowledge and tools to confidently tackle this and similar mixed fractions.
Introduction: What is 1 3/14?
The fraction 1 3/14 is a mixed fraction. This means it combines a whole number (1) and a proper fraction (3/14). A proper fraction has a numerator (top number, 3) that is smaller than its denominator (bottom number, 14). This indicates a quantity less than one whole unit. Therefore, 1 3/14 represents one whole unit plus three-fourteenths of another unit. Understanding mixed fractions is essential in various contexts, from everyday tasks like cooking and measuring to more complex mathematical calculations and scientific applications.
Representing 1 3/14 in Different Forms
1 3/14 can be represented in several ways, each useful in different circumstances:
-
Mixed Fraction: This is the form we've already encountered: 1 3/14. It's intuitive and easy to visualize.
-
Improper Fraction: An improper fraction has a numerator greater than or equal to its denominator. To convert 1 3/14 to an improper fraction, we multiply the whole number (1) by the denominator (14) and add the numerator (3): (1 * 14) + 3 = 17. This becomes the new numerator, keeping the original denominator: 17/14.
-
Decimal: To represent 1 3/14 as a decimal, we divide the numerator of the improper fraction (17) by the denominator (14): 17 ÷ 14 ≈ 1.214. Note that this is an approximation because the decimal representation of 3/14 is non-terminating (it goes on forever).
-
Percentage: To express 1 3/14 as a percentage, we convert the decimal approximation (1.214) to a percentage by multiplying by 100: 1.214 * 100 ≈ 121.4%.
Step-by-Step Conversion Examples
Let's illustrate the conversions in more detail:
1. Mixed Fraction to Improper Fraction:
- Multiply the whole number by the denominator: 1 * 14 = 14
- Add the numerator to the result: 14 + 3 = 17
- Keep the original denominator: 17/14
2. Improper Fraction to Decimal:
- Divide the numerator by the denominator: 17 ÷ 14 ≈ 1.214
3. Decimal to Percentage:
- Multiply the decimal by 100: 1.214 * 100 = 121.4%
Practical Applications of 1 3/14
While 1 3/14 might seem like an abstract mathematical concept, its application is far-reaching:
-
Measurement: Imagine measuring ingredients for a recipe. You might need 1 3/14 cups of flour or 1 3/14 inches of ribbon.
-
Data Analysis: In statistics, fractions like 1 3/14 might represent proportions or ratios within a dataset.
-
Time Management: If a task takes 1 3/14 hours, understanding this fraction is crucial for planning and scheduling.
-
Construction and Engineering: Precision measurements are essential, and fractions play a significant role. A blueprint might specify dimensions using fractions.
-
Finance: Calculating interest rates or proportions of investments often involves fractional values.
The Mathematical Concepts Behind 1 3/14
Understanding 1 3/14 requires familiarity with several core mathematical concepts:
-
Numerator and Denominator: The numerator (3) represents the number of parts you have, and the denominator (14) represents the total number of equal parts in a whole.
-
Proper and Improper Fractions: A proper fraction (like 3/14) has a smaller numerator than the denominator, while an improper fraction (like 17/14) has a larger or equal numerator.
-
Mixed Numbers: Mixed numbers combine a whole number and a proper fraction, as seen in 1 3/14.
-
Equivalent Fractions: These are fractions that represent the same value but have different numerators and denominators. For example, 1/2 is equivalent to 7/14. Finding equivalent fractions can simplify calculations.
-
Simplifying Fractions: Simplifying, or reducing, a fraction involves dividing both the numerator and the denominator by their greatest common divisor. Since 3 and 14 have no common divisors other than 1, 3/14 is already in its simplest form.
Frequently Asked Questions (FAQ)
-
Q: How do I add or subtract mixed fractions?
- A: Convert the mixed fractions to improper fractions first. Then, find a common denominator and add or subtract the numerators. Finally, convert the result back to a mixed fraction if necessary.
-
Q: How do I multiply or divide mixed fractions?
- A: Convert the mixed fractions to improper fractions. Then perform the multiplication or division as you would with regular fractions. Remember to simplify the result if possible.
-
Q: What is the reciprocal of 1 3/14?
- A: First, convert 1 3/14 to an improper fraction (17/14). The reciprocal is found by flipping the fraction, resulting in 14/17.
-
Q: Can 1 3/14 be expressed as a ratio?
- A: Yes, 1 3/14 can be expressed as a ratio. Using the improper fraction form (17/14), the ratio is 17:14. This indicates a relationship between two quantities.
Conclusion: Mastering the Fundamentals
Understanding fractions like 1 3/14 is fundamental to mathematical proficiency. By mastering the concepts of proper and improper fractions, mixed numbers, conversions, and basic operations, you'll build a strong foundation for more advanced mathematical concepts. This knowledge is not confined to the classroom; it extends to numerous practical applications in daily life and various professional fields. Remember to practice regularly and break down complex problems into smaller, manageable steps. With consistent effort and a clear understanding of the underlying principles, you'll confidently navigate the world of fractions and unlock their practical potential.
Latest Posts
Latest Posts
-
Beatles Who Is Still Alive
Sep 24, 2025
-
Do Latinas Like White Guys
Sep 24, 2025
-
1 X 2 X 4
Sep 24, 2025
-
How To Become Straight Again
Sep 24, 2025
-
Are There Lions In Australia
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Of 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.