1 X 1 0 X
vittoremobilya
Sep 24, 2025 · 7 min read
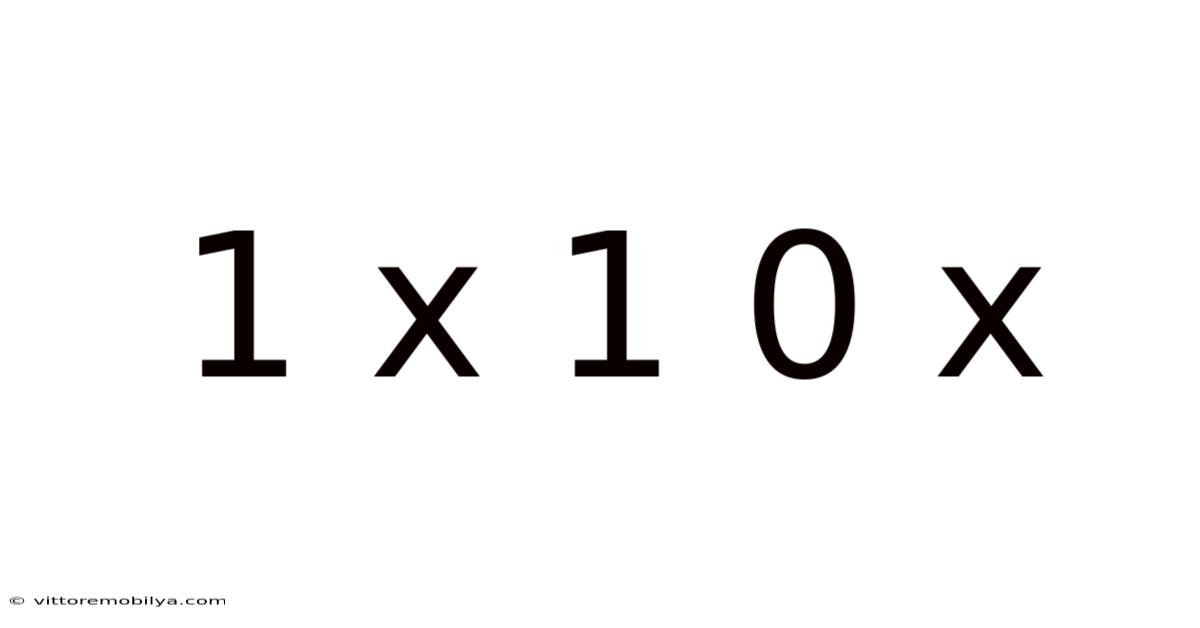
Table of Contents
Decoding 1 x 1 = 0: Exploring the World of Boolean Algebra and Logic Gates
The seemingly simple equation, 1 x 1 = 0, initially appears contradictory to basic arithmetic. However, this expression finds its validity within the fascinating realm of Boolean algebra, a system of algebra where variables can only take on two values: 0 (false) and 1 (true). This article delves into the concepts underlying this equation, exploring its significance in digital logic, computer science, and the foundation of modern computing. Understanding Boolean algebra is crucial for anyone interested in how computers work, from software developers to hardware engineers.
Introduction to Boolean Algebra
Boolean algebra, named after mathematician George Boole, is a type of algebra that deals with logical operations rather than numerical calculations. It forms the bedrock of digital electronics and computer science, providing a mathematical framework for designing and analyzing digital circuits. Unlike traditional algebra, where variables can represent a range of numerical values, Boolean variables are binary, representing either true (1) or false (0).
The fundamental operations in Boolean algebra are:
-
AND: The AND operation (represented by ⋅ or ∧) yields true (1) only if both inputs are true. Otherwise, it returns false (0). For example, 1 ⋅ 1 = 1, but 1 ⋅ 0 = 0, 0 ⋅ 1 = 0, and 0 ⋅ 0 = 0.
-
OR: The OR operation (represented by + or ∨) yields true (1) if at least one of the inputs is true. It only returns false (0) if both inputs are false. For example, 1 + 1 = 1, 1 + 0 = 1, 0 + 1 = 1, and 0 + 0 = 0.
-
NOT: The NOT operation (represented by ¬ or ') inverts the input. If the input is true (1), the output is false (0), and vice versa. For example, ¬1 = 0 and ¬0 = 1.
These three operations – AND, OR, and NOT – are the building blocks of all Boolean expressions and form the basis for designing logic gates.
Understanding Logic Gates
Logic gates are the fundamental building blocks of digital circuits. They implement the Boolean operations described above, taking one or more binary inputs and producing a single binary output. The most common logic gates are:
-
AND Gate: An AND gate outputs 1 only when both inputs are 1.
-
OR Gate: An OR gate outputs 1 if at least one input is 1.
-
NOT Gate (Inverter): A NOT gate inverts the input; if the input is 0, the output is 1, and vice-versa.
-
XOR (Exclusive OR) Gate: An XOR gate outputs 1 if only one input is 1 (but not both).
-
NAND Gate (NOT AND): A NAND gate is an AND gate followed by a NOT gate. It outputs 0 only when both inputs are 1.
-
NOR Gate (NOT OR): A NOR gate is an OR gate followed by a NOT gate. It outputs 1 only when both inputs are 0.
How 1 x 1 = 0 is Possible in Boolean Algebra
Now, let's revisit the equation 1 x 1 = 0. In standard arithmetic, this is obviously false. However, within the context of Boolean algebra, this equation can be true if the 'x' symbol represents a specific Boolean operation, specifically the NAND operation.
Remember, the NAND operation is equivalent to an AND operation followed by a NOT operation. So, if we interpret 'x' as the NAND operation, the equation becomes:
1 NAND 1 = 0
Let's break it down:
- The AND operation of 1 and 1 is 1 (1 ⋅ 1 = 1).
- The NOT operation inverts the result of the AND operation. Therefore, NOT(1) = 0.
Thus, in Boolean algebra, using the NAND operation, the equation 1 x 1 = 0 holds true. This demonstrates how the interpretation of symbols and operations is crucial when working within different algebraic systems.
Applications of Boolean Algebra and Logic Gates
The applications of Boolean algebra and logic gates are vast and pervasive in modern technology. They form the foundation of:
-
Digital Circuits: Boolean algebra is used to design and analyze digital circuits, which are the building blocks of computers, smartphones, and other digital devices. Every operation within a computer, from arithmetic calculations to data storage, is ultimately implemented using logic gates.
-
Computer Arithmetic: Boolean algebra provides the framework for implementing arithmetic operations (addition, subtraction, multiplication, division) in computers. These operations are broken down into sequences of Boolean operations performed by logic gates.
-
Data Storage and Retrieval: Memory chips in computers use logic gates to store and retrieve data. The presence or absence of electrical charge represents the binary values 1 and 0.
-
Control Systems: Boolean logic is crucial in designing control systems, such as those used in industrial automation, robotics, and traffic lights. These systems use Boolean expressions to make decisions based on input conditions.
-
Software Development: Although programmers rarely work directly with logic gates, the underlying principles of Boolean algebra influence programming languages and how programs process data and make decisions. Conditional statements (if-else statements) in programming languages directly reflect Boolean logic.
Beyond Simple Gates: Complex Boolean Expressions
While basic logic gates provide the fundamental building blocks, more complex circuits and functionalities require combining multiple gates to implement more intricate Boolean expressions. These expressions can be simplified using Boolean algebra theorems and laws, making circuits more efficient and smaller. Some of these simplification techniques include:
- Commutative Laws: A + B = B + A and A ⋅ B = B ⋅ A
- Associative Laws: (A + B) + C = A + (B + C) and (A ⋅ B) ⋅ C = A ⋅ (B ⋅ C)
- Distributive Laws: A ⋅ (B + C) = (A ⋅ B) + (A ⋅ C) and A + (B ⋅ C) = (A + B) ⋅ (A + C)
- De Morgan's Laws: ¬(A + B) = ¬A ⋅ ¬B and ¬(A ⋅ B) = ¬A + ¬B
By applying these laws, complex Boolean expressions can be simplified, leading to more efficient and cost-effective circuit designs. This simplification is a crucial part of digital circuit design.
Truth Tables and Karnaugh Maps
Two essential tools used in Boolean algebra are truth tables and Karnaugh maps.
-
Truth Tables: A truth table systematically lists all possible input combinations for a Boolean expression and their corresponding output values. It's a fundamental method for verifying the functionality of a Boolean expression or a logic circuit.
-
Karnaugh Maps (K-maps): K-maps are graphical tools used to simplify Boolean expressions. They provide a visual way to identify redundant terms and minimize the number of logic gates required for a given function. This leads to more efficient circuit designs.
Frequently Asked Questions (FAQ)
Q: Is Boolean algebra only used in computer science?
A: While heavily used in computer science and digital electronics, Boolean algebra has broader applications. It’s used in areas like set theory, mathematical logic, and even some aspects of artificial intelligence and database design.
Q: How are Boolean expressions implemented in hardware?
A: Boolean expressions are implemented in hardware using combinations of logic gates. Each gate performs a specific Boolean operation (AND, OR, NOT, etc.), and their interconnection defines the overall function of the circuit.
Q: Can Boolean algebra handle more than two values?
A: While standard Boolean algebra is binary (0 and 1), extensions exist, like multi-valued logic, which can handle more than two values. However, the fundamental principles remain similar.
Q: What are some examples of real-world applications beyond computers?
A: Boolean logic finds its way into everyday systems such as traffic light controllers, home security systems, and even some aspects of industrial process control.
Q: How difficult is it to learn Boolean algebra?
A: The basic concepts are relatively straightforward to grasp. However, mastering the simplification techniques and applying them to complex circuits requires practice and understanding.
Conclusion
The equation 1 x 1 = 0, initially perplexing, finds its logical validity within the framework of Boolean algebra. Understanding this seemingly contradictory equation opens a gateway into the fascinating world of digital logic, a world that underpins modern computing and countless technological advancements. By mastering the fundamentals of Boolean algebra and logic gates, one gains a deeper appreciation of the intricate workings of digital systems and their immense impact on our lives. The principles discussed here are fundamental for anyone pursuing a career in computer science, electrical engineering, or any field reliant on digital technology. From the simplest logic gate to the most complex computer systems, Boolean algebra remains the silent yet powerful force driving the digital revolution.
Latest Posts
Latest Posts
-
Classes For Adults Near Me
Sep 24, 2025
-
3 4 Magnitude Earthquake Hits Auburn Washington
Sep 24, 2025
-
Strapless Bra For Large Breasts
Sep 24, 2025
-
Texas Roadhouse Delivery Near Me
Sep 24, 2025
-
Mark Ronson Uptown Funk Lyrics
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 1 X 1 0 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.