2/3 Is Greater Than 1/2
vittoremobilya
Sep 16, 2025 · 5 min read
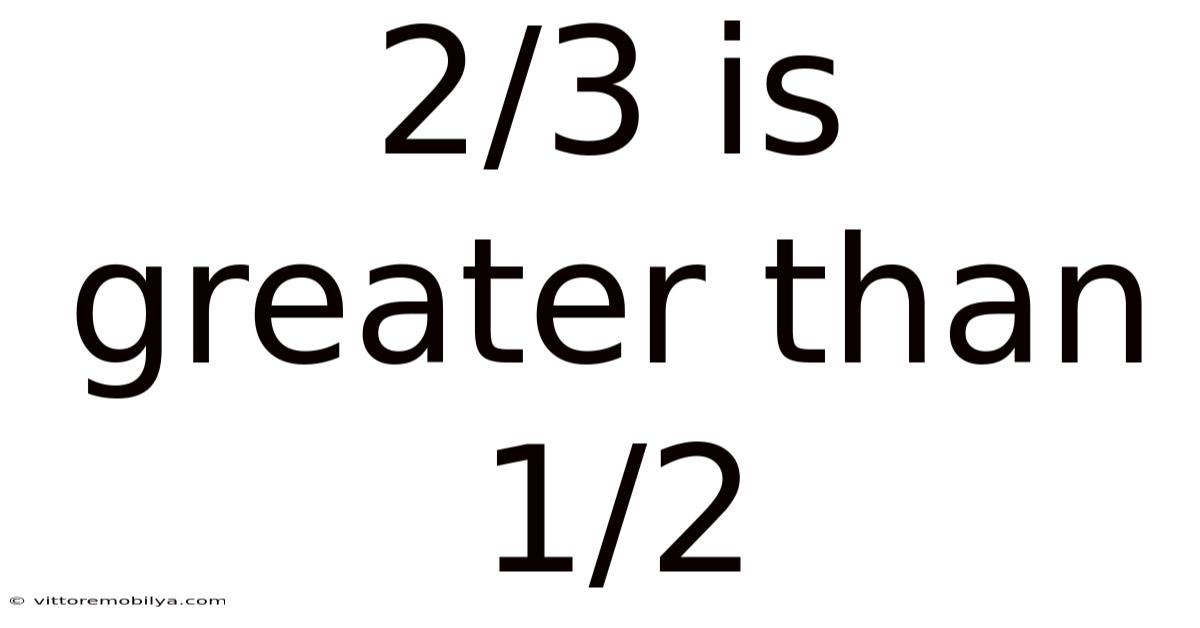
Table of Contents
2/3 is Greater Than 1/2: A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for navigating everyday life from cooking to budgeting. One common point of confusion, especially for beginners, is comparing the relative size of fractions. This article provides a comprehensive explanation of why 2/3 is greater than 1/2, exploring various methods to compare fractions and addressing common misconceptions. We'll delve into the underlying mathematical principles, offering multiple approaches to solidify your understanding and build confidence in tackling fraction comparisons.
Introduction: The Basics of Fractions
Before jumping into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts we are considering.
For example, in the fraction 2/3, the denominator (3) tells us the whole is divided into three equal parts, and the numerator (2) indicates that we're focusing on two of those parts. Similarly, in the fraction 1/2, the whole is divided into two equal parts, and we are considering one of them.
Method 1: Visual Representation
The simplest way to understand why 2/3 is greater than 1/2 is through visual representation. Imagine two identical pies.
- Pie 1: Cut the first pie into three equal slices. Take two of those slices (2/3).
- Pie 2: Cut the second pie into two equal slices. Take one of those slices (1/2).
By visually comparing the amount of pie you have from each, it becomes clear that two slices out of three (2/3) represent a larger portion than one slice out of two (1/2). This visual approach helps to build an intuitive understanding of the concept.
Method 2: Finding a Common Denominator
A more formal mathematical approach involves finding a common denominator. This means converting both fractions so they have the same denominator, allowing for direct comparison of the numerators.
The least common multiple (LCM) of 2 and 3 is 6. Therefore, we convert both fractions to have a denominator of 6:
- Converting 1/2: To change the denominator from 2 to 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
- Converting 2/3: To change the denominator from 3 to 6, we multiply both the numerator and the denominator by 2: (2 x 2) / (3 x 2) = 4/6
Now we have 3/6 and 4/6. Since both fractions have the same denominator, we can directly compare the numerators: 4 > 3. Therefore, 4/6 (which is equivalent to 2/3) is greater than 3/6 (which is equivalent to 1/2).
Method 3: Decimal Conversion
Another effective method is converting both fractions into decimals. This allows for a straightforward numerical comparison.
- Converting 1/2: Divide the numerator (1) by the denominator (2): 1 ÷ 2 = 0.5
- Converting 2/3: Divide the numerator (2) by the denominator (3): 2 ÷ 3 ≈ 0.667
Comparing the decimal values, 0.667 > 0.5, confirming that 2/3 is greater than 1/2.
Method 4: Using a Number Line
Representing fractions on a number line provides a visual and numerical understanding of their relative positions. A number line from 0 to 1, divided into equal segments, can clearly show that 2/3 lies to the right of 1/2, indicating it is the larger fraction. This method combines visual and numerical approaches for a comprehensive understanding.
Understanding the Underlying Principles
The methods above all rely on the fundamental principle that when the denominators are the same, the fraction with the larger numerator is the larger fraction. When the numerators are the same, the fraction with the smaller denominator is the larger fraction. These rules are core to understanding fraction comparison. Furthermore, it's crucial to remember that equivalent fractions represent the same value. For instance, 1/2, 2/4, 3/6, and so on, are all equivalent fractions representing the same portion of a whole.
Addressing Common Misconceptions
A common misconception is focusing solely on the numerators or denominators without considering the relationship between them. Simply seeing that 2 (in 2/3) is larger than 1 (in 1/2) does not automatically make 2/3 larger. The denominator plays a crucial role in determining the size of the fraction.
Another misconception is incorrectly assuming that the larger the numbers in a fraction, the larger the fraction itself. This is not true. For example, while 10/20 appears larger in terms of the numbers involved than 1/2, they are equivalent fractions both representing one-half.
Practical Applications
Understanding fraction comparison has numerous practical applications in daily life. From following recipes (measuring ingredients) to calculating discounts or understanding proportions in construction or engineering, comparing fractions is a vital skill across various fields.
Frequently Asked Questions (FAQ)
-
Q: Are there other methods to compare fractions besides the ones mentioned? A: Yes, there are more advanced methods, especially for comparing multiple fractions or fractions with larger numbers. These often involve simplifying fractions to their lowest terms or using cross-multiplication.
-
Q: What if I have fractions with different signs (positive and negative)? A: When dealing with negative fractions, the comparison changes. A larger negative fraction is actually smaller in value than a smaller negative fraction. For example, -2/3 is less than -1/2.
-
Q: How can I improve my skills in comparing fractions? A: Practice is key! Work through various examples, using different methods, and gradually increase the complexity of the fractions you compare.
Conclusion: Mastering Fraction Comparison
Understanding why 2/3 is greater than 1/2 is a stepping stone to mastering fraction comparison. Through visual representation, finding common denominators, decimal conversion, and using a number line, we've explored multiple approaches to solidify this understanding. By grasping the underlying principles and addressing common misconceptions, you can build confidence in comparing fractions and apply this crucial skill to various real-world scenarios. Remember, consistent practice and a clear understanding of the fundamentals are essential for success in mastering fractions. Keep practicing, and you'll soon find yourself confidently navigating the world of fractions.
Latest Posts
Latest Posts
-
X 2 Y 2 X
Sep 17, 2025
-
Four Arms In Ben 10
Sep 17, 2025
-
Claw Clips For Thick Hair
Sep 17, 2025
-
How To Kill Vengeance Spirits
Sep 17, 2025
-
Csu San Bernardino Vs Fullerton
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 2/3 Is Greater Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.