3 3/8 As A Decimal
vittoremobilya
Sep 25, 2025 · 5 min read
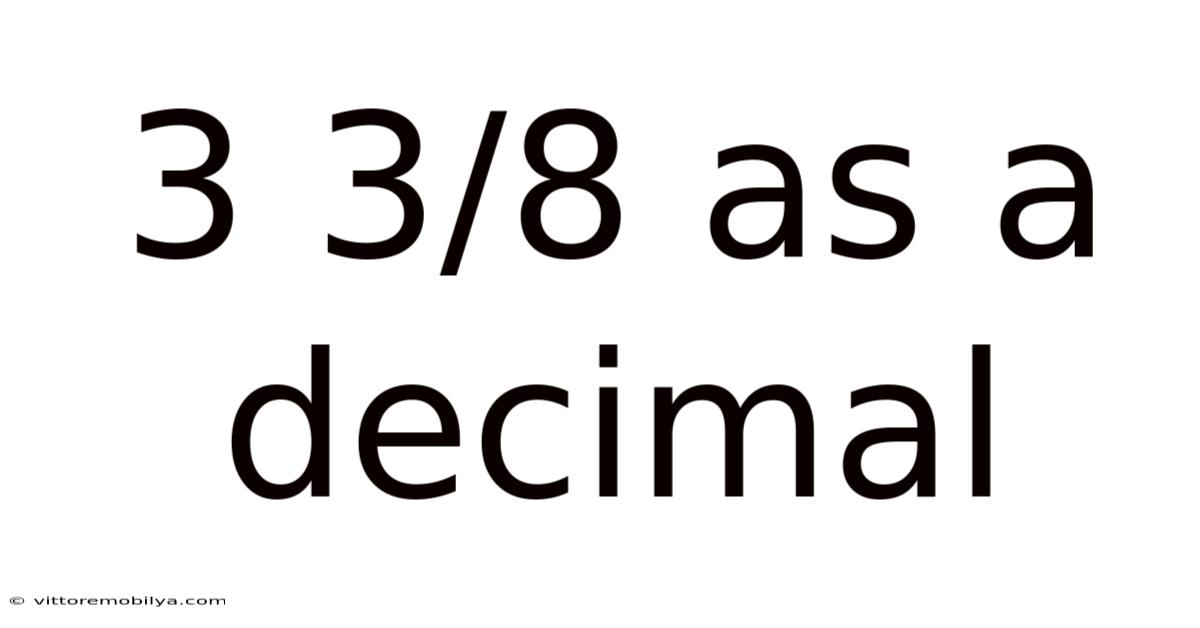
Table of Contents
Decoding 3 3/8 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the mixed number 3 3/8 into its decimal equivalent, providing a detailed explanation suitable for learners of all levels. We'll cover various methods, explore the underlying concepts, and address common questions, ensuring a complete understanding of this seemingly simple yet crucial conversion. This guide will cover not only the practical steps but also the theoretical underpinnings, making it a valuable resource for anyone looking to master fraction-to-decimal conversions.
Understanding Mixed Numbers and Decimals
Before diving into the conversion, let's briefly review the concepts of mixed numbers and decimals. A mixed number combines a whole number and a fraction, like 3 3/8. The whole number (3 in this case) represents complete units, while the fraction (3/8) represents a portion of a unit.
A decimal, on the other hand, represents a number using a base-ten system, where digits to the right of the decimal point represent fractions with denominators of powers of 10 (tenths, hundredths, thousandths, etc.). For example, 0.5 represents one-half (1/2), and 0.25 represents one-quarter (1/4).
Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number
This is arguably the most straightforward method. We'll break down the conversion into two steps:
Step 1: Convert the fraction 3/8 to a decimal.
To convert a fraction to a decimal, we divide the numerator (the top number) by the denominator (the bottom number). In this case:
3 ÷ 8 = 0.375
Step 2: Add the whole number.
Now, simply add the whole number part of the mixed number (3) to the decimal equivalent of the fraction (0.375):
3 + 0.375 = 3.375
Therefore, 3 3/8 as a decimal is 3.375.
Method 2: Converting the Entire Mixed Number Directly
This method involves converting the entire mixed number into an improper fraction first, then dividing to obtain the decimal.
Step 1: Convert the mixed number to an improper fraction.
To convert a mixed number to an improper fraction, we multiply the whole number by the denominator of the fraction and add the numerator. This result becomes the new numerator, while the denominator remains the same.
(3 x 8) + 3 = 27
So, 3 3/8 becomes 27/8.
Step 2: Convert the improper fraction to a decimal.
Now, divide the numerator by the denominator:
27 ÷ 8 = 3.375
Again, we arrive at the same answer: 3.375.
Understanding the Decimal Places: Tenths, Hundredths, Thousandths
The decimal 3.375 has three digits after the decimal point. These digits represent:
- 3 in the tenths place (3/10)
- 7 in the hundredths place (7/100)
- 5 in the thousandths place (5/1000)
This means that 3.375 can also be expressed as: 3 + 3/10 + 7/100 + 5/1000.
The Significance of Decimal Representation
Converting fractions to decimals offers several advantages:
- Easier Comparison: Decimals allow for easier comparison of numbers. For example, it's simpler to compare 3.375 and 3.4 than 3 3/8 and 3 4/10.
- Calculations: Many calculations, particularly those involving multiplication and division, are often easier to perform with decimals than with fractions.
- Real-World Applications: Decimals are extensively used in various real-world applications, including finance, engineering, and science. Measurements, for instance, are frequently expressed in decimal form.
Addressing Common Questions and Misconceptions
Q: Can all fractions be converted to terminating decimals?
A: No. Fractions with denominators that have prime factors other than 2 and 5 will result in repeating decimals (e.g., 1/3 = 0.333...). However, 3 3/8 has a denominator of 8 (2 x 2 x 2), which only contains the prime factor 2, leading to a terminating decimal.
Q: What if I made a mistake in the division?
A: Using a calculator can minimize the risk of errors, especially when dealing with larger numbers or more complex fractions. However, understanding the underlying process is crucial, allowing you to identify and correct any errors manually. Double-checking your calculations is always a good practice.
Q: Are there other methods for converting fractions to decimals?
A: While the methods described above are the most common and straightforward, other methods exist, particularly involving the use of equivalent fractions or long division. However, the methods described provide a clear and efficient approach.
Q: Why is it important to learn this conversion?
A: Mastering fraction-to-decimal conversion is essential for various reasons: It enhances your overall understanding of numbers, facilitates mathematical computations, improves problem-solving skills across multiple disciplines, and prepares you for more advanced mathematical concepts.
Expanding on the Concept: Working with More Complex Mixed Numbers
The principles demonstrated above can be applied to convert any mixed number to its decimal equivalent. For example, let's consider converting 5 17/20:
Step 1: Convert the fraction 17/20 to a decimal:
17 ÷ 20 = 0.85
Step 2: Add the whole number:
5 + 0.85 = 5.85
Therefore, 5 17/20 as a decimal is 5.85.
Similarly, you can apply these methods to convert any mixed number. The key is to understand the core principle of dividing the numerator by the denominator and then adding the whole number.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting 3 3/8 to its decimal equivalent, 3.375, is a fundamental skill in mathematics with widespread practical applications. By understanding the various methods and their underlying principles, you'll gain confidence in handling fraction-to-decimal conversions, a crucial skill that will serve you well in numerous academic and real-world scenarios. Remember to practice regularly and don’t hesitate to revisit the steps if needed. With consistent effort, you'll master this important skill and build a strong foundation in mathematical understanding. The ability to seamlessly translate between fractions and decimals is a testament to a solid grasp of numerical concepts and an invaluable tool in various mathematical and practical applications.
Latest Posts
Latest Posts
-
Fly Houston To Los Angeles
Sep 25, 2025
-
50 Amp Rv Extension Cord
Sep 25, 2025
-
What To Serve With Lasagna
Sep 25, 2025
-
3 Ton Air Conditioning Unit
Sep 25, 2025
-
I Love You In Greek
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 3 3/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.