3 4 Cup Times 4
vittoremobilya
Sep 13, 2025 · 5 min read
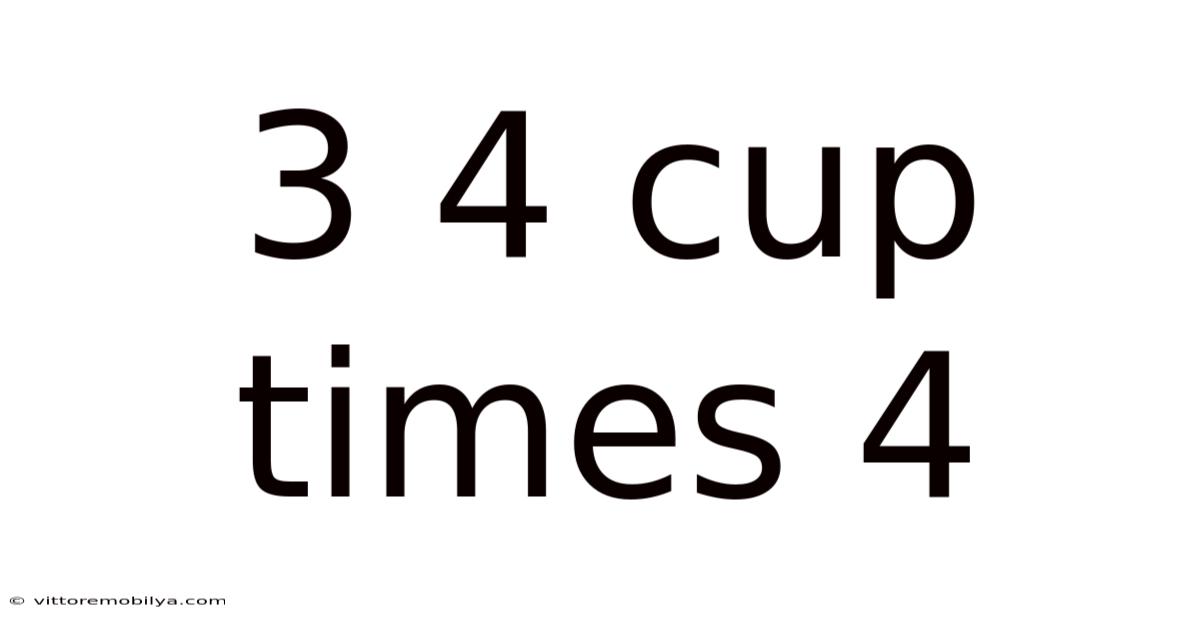
Table of Contents
Decoding 3/4 Cup Times 4: A Deep Dive into Fraction Multiplication
Understanding fractions is a fundamental skill in mathematics, crucial for everyday tasks and advanced studies alike. This article will comprehensively explore the calculation of 3/4 cup times 4, delving beyond the simple answer to uncover the underlying principles and practical applications. We'll cover various methods for solving this problem, explain the underlying mathematical concepts, and explore real-world scenarios where this type of calculation is essential. Whether you're a student brushing up on your fractions or a home cook needing to accurately measure ingredients, this guide will equip you with a thorough understanding.
Understanding the Problem: 3/4 Cup Times 4
The problem "3/4 cup times 4" asks us to determine the total quantity when four groups of ¾ cup are combined. This involves multiplying a fraction (3/4) by a whole number (4). While seemingly simple, mastering this calculation is key to understanding more complex fraction operations. It's a common problem encountered in cooking, baking, and various scientific or engineering contexts requiring precise measurements.
Method 1: Direct Multiplication
The most straightforward method involves directly multiplying the numerator (the top number) of the fraction by the whole number, keeping the denominator (the bottom number) the same.
- Step 1: Multiply the numerator by the whole number: 3 x 4 = 12
- Step 2: Keep the denominator the same: The denominator remains 4.
- Step 3: Simplify the resulting fraction: 12/4 simplifies to 3.
Therefore, 3/4 cup times 4 equals 3 cups.
Method 2: Visual Representation
Visual aids can make understanding fraction multiplication more intuitive, especially for visual learners. Imagine four separate containers, each holding ¾ cup of a substance.
- Representation: Draw four circles, each divided into four equal parts. Shade three parts in each circle to represent ¾ cup.
- Combining: Count the total number of shaded parts. You'll have 12 shaded parts in total.
- Conversion: Since each circle represents one whole cup (divided into four equal parts), 12 shaded parts represent 12/4 cups, which simplifies to 3 cups.
This visual method provides a concrete understanding of how the multiplication works and reinforces the concept of combining fractional parts.
Method 3: Converting to Decimal
Converting fractions to decimals can sometimes simplify calculations. To do this, divide the numerator by the denominator.
- Conversion: 3 ÷ 4 = 0.75
- Multiplication: 0.75 x 4 = 3
This method confirms that 3/4 cup times 4 is equal to 3 cups. While efficient for this specific problem, it might be less intuitive for understanding the underlying principles of fraction multiplication.
The Mathematical Principles at Play
The calculation of 3/4 cup times 4 demonstrates fundamental principles of fraction multiplication:
- Multiplication of Fractions: When multiplying a fraction by a whole number, we multiply the numerator of the fraction by the whole number and keep the denominator the same.
- Simplifying Fractions: After multiplication, it's crucial to simplify the resulting fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. In our example, the GCD of 12 and 4 is 4, leading to the simplified fraction 3/1, which is equal to 3.
- Equivalent Fractions: The process of simplifying fractions demonstrates the concept of equivalent fractions. 12/4 and 3/1 represent the same quantity, just expressed in different forms.
Real-World Applications
Understanding fraction multiplication with real numbers is crucial in many practical situations:
- Cooking and Baking: Recipes frequently require precise measurements. If a recipe calls for ¾ cup of flour per serving and you need to make four servings, you'll need to calculate ¾ cup x 4 = 3 cups of flour.
- Construction and Engineering: Precise measurements are critical in construction and engineering projects. Calculating the amount of materials needed often involves multiplying fractions.
- Science Experiments: Many scientific experiments require precise measurements of liquids or other materials, frequently involving fractions and their multiplication.
- Finance and Budgeting: Calculating portions of a budget or determining discounts often involves working with fractions.
Frequently Asked Questions (FAQ)
Q: What if the whole number wasn't 4? How would I calculate 3/4 cup times 5?
A: The process remains the same. Multiply the numerator (3) by the whole number (5): 3 x 5 = 15. Keep the denominator (4) the same: 15/4. This simplifies to 3 ¾ cups.
Q: Can I multiply fractions by fractions?
A: Yes, absolutely. When multiplying fractions by other fractions, you multiply the numerators together and the denominators together. For instance, (1/2) x (2/3) = (1x2)/(2x3) = 2/6, which simplifies to 1/3.
Q: What if the fraction was a mixed number (e.g., 1 ¾)?
A: You would first convert the mixed number into an improper fraction. For 1 ¾, the improper fraction is 7/4. Then you proceed with the multiplication as before. For example, 1 ¾ cups times 2 would be (7/4) x 2 = 14/4, which simplifies to 3 ½ cups.
Q: Are there any online tools or calculators that can help with fraction multiplication?
A: Yes, many online calculators are available that can perform fraction multiplication and other mathematical operations. However, understanding the underlying concepts is crucial for applying these calculations correctly in various contexts.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication, such as calculating 3/4 cup times 4, is essential for success in various academic and real-world scenarios. By understanding the underlying mathematical principles and practicing different methods, you can build confidence and proficiency in working with fractions. Whether through direct multiplication, visual representation, or decimal conversion, the result remains consistent: 3/4 cup times 4 equals 3 cups. This seemingly simple calculation highlights the importance of precise measurement and fundamental mathematical understanding in everyday life. Remember to always simplify your fractions to their lowest terms for clarity and accuracy. Continued practice and a clear understanding of the concepts will equip you with the skills to tackle more complex fraction problems confidently.
Latest Posts
Latest Posts
-
Best Stretch Mark Laser Removal
Sep 13, 2025
-
I Love My Boyfriend Shirt
Sep 13, 2025
-
13mm Is What In Inches
Sep 13, 2025
-
How Long Did It Take
Sep 13, 2025
-
Phlebotomy Jobs Hiring Near Me
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Cup Times 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.