Factorizar 2x 2 7x 3
vittoremobilya
Sep 18, 2025 · 6 min read
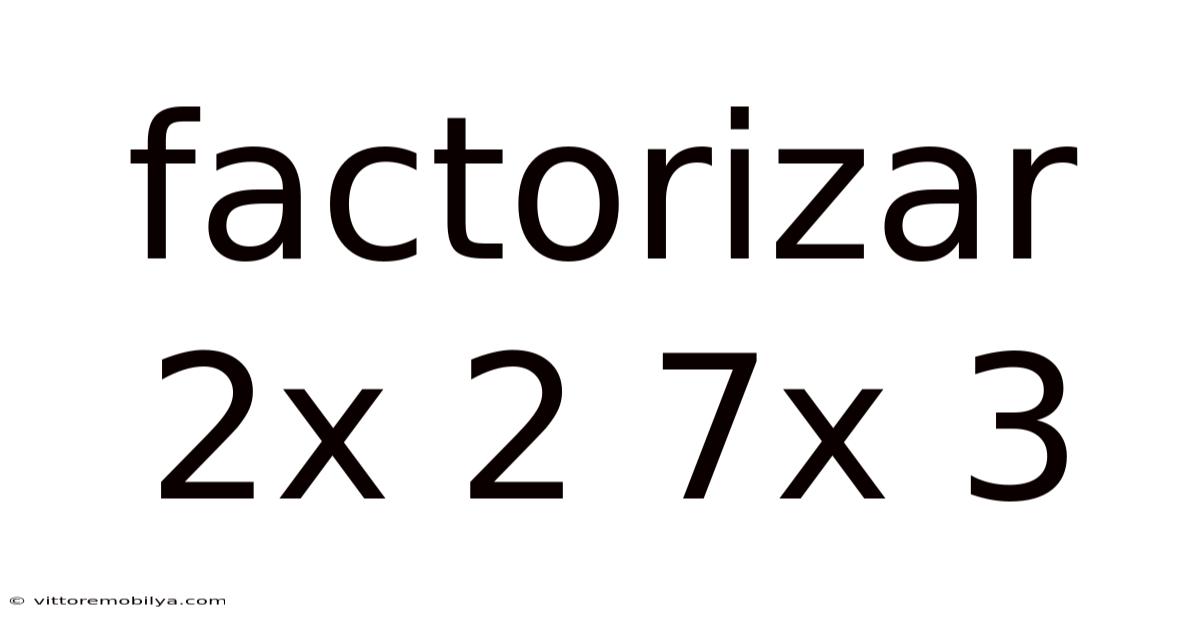
Table of Contents
Factoring Quadratic Expressions: A Deep Dive into 2x² + 7x + 3
Factoring quadratic expressions is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding various mathematical concepts. This article provides a comprehensive guide to factoring the specific quadratic expression 2x² + 7x + 3, while also exploring the broader techniques applicable to a wide range of quadratic equations. We'll delve into the process step-by-step, explain the underlying mathematical principles, and address frequently asked questions. Understanding this process will significantly enhance your algebraic abilities.
Introduction: Understanding Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (typically 'x') is 2. It generally takes the form ax² + bx + c, where 'a', 'b', and 'c' are constants. Factoring a quadratic expression means rewriting it as a product of two simpler expressions, usually two binomials. This process is the reverse of expanding binomials using the distributive property (often referred to as FOIL). Our focus here is on factoring 2x² + 7x + 3.
Step-by-Step Factoring of 2x² + 7x + 3
There are several methods to factor quadratic expressions. For 2x² + 7x + 3, we'll employ the most common technique, which involves finding two numbers that satisfy specific criteria.
1. Identify 'a', 'b', and 'c':
In our expression, 2x² + 7x + 3, we have:
- a = 2
- b = 7
- c = 3
2. Find Two Numbers:
We need to find two numbers that:
- Multiply to equal the product of 'a' and 'c' (ac = 2 * 3 = 6).
- Add up to 'b' (b = 7).
Let's consider the factors of 6: 1 and 6, 2 and 3, -1 and -6, -2 and -3. The pair 1 and 6 satisfies the second condition (1 + 6 = 7).
3. Rewrite the Middle Term:
Now, we rewrite the middle term (7x) using the two numbers we found (1 and 6):
2x² + 1x + 6x + 3
4. Factor by Grouping:
We group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
x(2x + 1) + 3(2x + 1)
Notice that (2x + 1) is a common factor in both terms.
5. Final Factored Form:
We factor out the common binomial (2x + 1):
(2x + 1)(x + 3)
Therefore, the factored form of 2x² + 7x + 3 is (2x + 1)(x + 3). You can verify this by expanding the factored form using the FOIL method: (2x + 1)(x + 3) = 2x² + 6x + x + 3 = 2x² + 7x + 3.
Alternative Method: Trial and Error
Another approach, especially useful for simpler quadratics, is trial and error. Since the leading coefficient is 2, the first terms of the binomials must be 2x and x (or x and 2x). The last terms must multiply to 3. Therefore, we can try different combinations until we find one that produces the correct middle term:
- (2x + 1)(x + 3) This gives 2x² + 7x + 3 (correct!)
- (2x + 3)(x + 1) This gives 2x² + 5x + 3 (incorrect)
- (2x - 1)(x - 3) This gives 2x² -7x + 3 (incorrect)
- (2x - 3)(x - 1) This gives 2x² -5x + 3 (incorrect)
This method can be faster for simpler expressions but might become less efficient for more complex quadratics.
The Significance of Factoring Quadratic Expressions
The ability to factor quadratic expressions is not merely an algebraic exercise; it has numerous applications across various mathematical fields and real-world problems:
-
Solving Quadratic Equations: Setting a quadratic expression equal to zero creates a quadratic equation. Factoring allows you to find the roots (solutions) of the equation by setting each factor to zero and solving for x. For example, solving 2x² + 7x + 3 = 0 leads to (2x + 1)(x + 3) = 0, giving solutions x = -1/2 and x = -3.
-
Simplifying Rational Expressions: Factoring is essential for simplifying rational expressions (fractions with polynomials). Common factors in the numerator and denominator can be canceled out, simplifying the expression.
-
Graphing Quadratic Functions: The factored form of a quadratic expression reveals the x-intercepts (where the graph crosses the x-axis) of the corresponding quadratic function. These intercepts are crucial for sketching the parabola.
-
Calculus Applications: Factoring plays a critical role in various calculus techniques, such as finding derivatives and integrals.
-
Real-World Modeling: Quadratic equations and their factored forms are used to model numerous real-world phenomena, including projectile motion, area calculations, and optimization problems.
Explanation of the Underlying Mathematical Principles
The process of factoring quadratic expressions relies on several fundamental algebraic principles:
-
Distributive Property: This property states that a(b + c) = ab + ac. Factoring is essentially the reverse of applying the distributive property.
-
Greatest Common Factor (GCF): Finding the GCF is crucial for simplifying expressions and grouping terms effectively during factoring.
-
Zero Product Property: This property states that if the product of two factors is zero, then at least one of the factors must be zero. This property is used to solve quadratic equations once they are factored.
-
Polynomial Division (Optional): In cases where factoring by grouping or trial and error proves difficult, polynomial long division can be employed to find factors.
Frequently Asked Questions (FAQ)
-
What if the quadratic expression cannot be factored? Not all quadratic expressions can be factored using integers. In such cases, the quadratic formula or completing the square can be used to find the roots.
-
Are there other methods for factoring quadratics? Yes, besides factoring by grouping and trial and error, other techniques include the quadratic formula, completing the square, and using specialized factoring formulas for specific types of quadratics (e.g., perfect square trinomials, difference of squares).
-
How can I improve my factoring skills? Practice is key! Work through numerous examples, starting with simpler expressions and gradually increasing the complexity. Familiarize yourself with different factoring techniques and understand the underlying principles.
-
What are some common mistakes to avoid when factoring? Common errors include incorrect sign assignments, overlooking common factors, and making arithmetic mistakes during calculations. Always double-check your work by expanding the factored form to ensure it matches the original expression.
Conclusion: Mastering Quadratic Factoring
Factoring quadratic expressions is a cornerstone of algebra, with applications extending far beyond classroom exercises. Understanding the step-by-step process, the underlying mathematical principles, and the various techniques available allows you to tackle a wide range of algebraic problems confidently. By practicing regularly and addressing common pitfalls, you'll develop proficiency in this essential skill, paving the way for success in more advanced mathematical studies and real-world applications. Remember, the key to mastering factoring is consistent practice and a solid grasp of the fundamental algebraic concepts. The ability to easily factor expressions like 2x² + 7x + 3 will significantly enhance your overall mathematical fluency and problem-solving capabilities.
Latest Posts
Latest Posts
-
Is A Bunny A Rodent
Sep 18, 2025
-
Hotels With Own Hot Tub
Sep 18, 2025
-
Washington State University Acceptance Rate
Sep 18, 2025
-
Query For Update In Sql
Sep 18, 2025
-
Words That Rhyme With It
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Factorizar 2x 2 7x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.