Half Of 1 1 2
vittoremobilya
Sep 25, 2025 · 5 min read
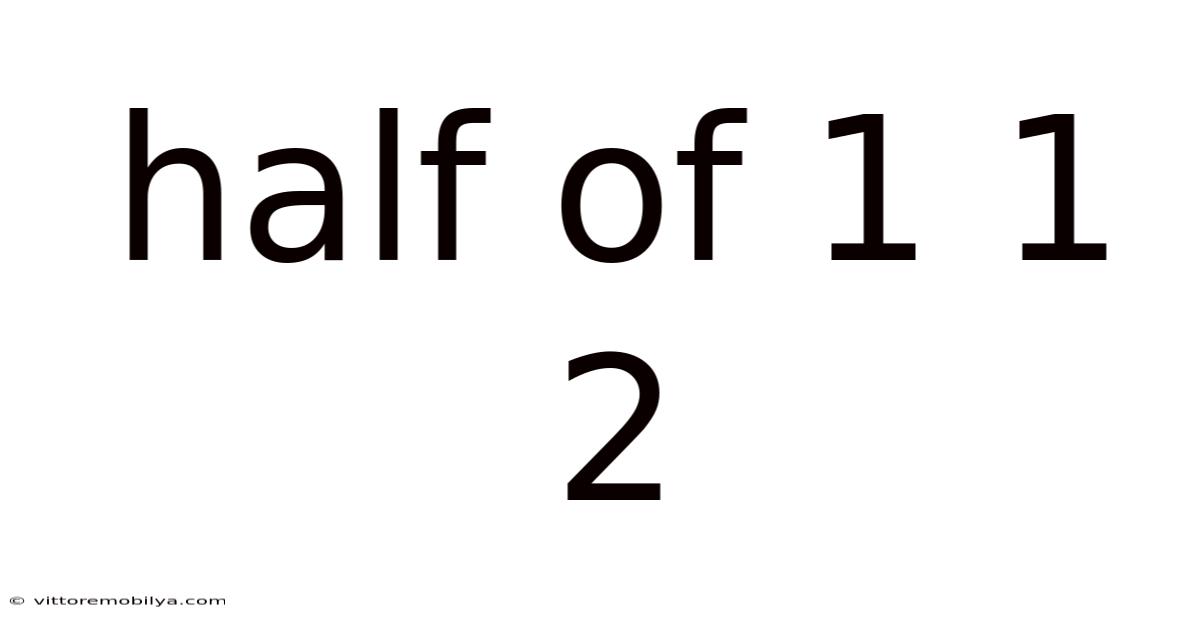
Table of Contents
Decoding "Half of 1 1 2": A Deep Dive into Fractions, Mixed Numbers, and Problem-Solving
This article explores the seemingly simple question, "What is half of 1 1 2?", but delves far beyond the immediate answer to illuminate fundamental mathematical concepts related to fractions, mixed numbers, and problem-solving strategies. We'll cover the various approaches to solving this problem, explain the underlying mathematical principles, and address common misconceptions. Understanding this seemingly simple problem provides a strong foundation for tackling more complex mathematical challenges.
Understanding the Question: "Half of 1 1 2"
The question "half of 1 1 2" essentially asks us to find one-half (1/2) of the quantity represented by "1 1 2". The number "1 1 2" is a mixed number, meaning it combines a whole number (1) and a proper fraction (1/2). This seemingly simple phrase involves several key mathematical concepts:
- Fractions: Fractions represent parts of a whole. In this case, we are working with the fraction 1/2, which represents one out of two equal parts.
- Mixed Numbers: Mixed numbers represent a combination of a whole number and a fraction. The number 1 1/2 represents one whole unit and one-half of another unit.
- Multiplication: Finding "half of" something is mathematically equivalent to multiplying by 1/2.
Method 1: Converting to an Improper Fraction
The most straightforward method involves converting the mixed number 1 1/2 into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator.
-
Convert the mixed number to an improper fraction: To do this, we multiply the whole number (1) by the denominator (2) and add the numerator (1). This gives us (1 * 2) + 1 = 3. The denominator remains the same (2). Therefore, 1 1/2 is equivalent to 3/2.
-
Multiply by 1/2: Now we multiply 3/2 by 1/2:
(3/2) * (1/2) = (3 * 1) / (2 * 2) = 3/4
Therefore, half of 1 1/2 is 3/4.
Method 2: Working with the Whole Number and Fraction Separately
We can also solve this problem by working with the whole number and the fractional part separately.
-
Find half of the whole number: Half of 1 is 1/2.
-
Find half of the fraction: Half of 1/2 is (1/2) * (1/2) = 1/4.
-
Combine the results: Add the two results together: 1/2 + 1/4. To add these fractions, we need a common denominator, which is 4. So we rewrite 1/2 as 2/4.
2/4 + 1/4 = 3/4
Again, we arrive at the answer: half of 1 1/2 is 3/4.
Method 3: Visual Representation
A visual approach can be particularly helpful for understanding the concept. Imagine a circle representing one whole unit. Divide this circle in half. 1 1/2 would then represent one whole circle and another half-circle. If you divide this entire quantity (1 and a half circles) in half again, you'll end up with three quarters of a circle. This visual representation clearly shows that half of 1 1/2 is 3/4.
Understanding the Concepts: Fractions and Mixed Numbers
This problem highlights the importance of understanding fractions and mixed numbers.
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
-
Mixed Numbers: A mixed number combines a whole number and a fraction. It represents a quantity that is greater than one. Converting a mixed number to an improper fraction, and vice versa, is a crucial skill in working with fractions.
Problem-Solving Strategies: A Broader Perspective
Solving "half of 1 1/2" showcases several essential problem-solving strategies:
-
Breaking down complex problems: We broke the problem down into smaller, more manageable parts (finding half of the whole number and half of the fraction separately).
-
Using multiple methods: We demonstrated multiple approaches to the problem, reinforcing understanding and showing different ways to arrive at the same solution.
-
Visual representation: The visual method provides an intuitive understanding of the concept, making it easier to grasp for learners.
-
Connecting concepts: The problem links the concepts of fractions, mixed numbers, and multiplication in a practical way.
Frequently Asked Questions (FAQ)
Q: Can I solve this using decimals?
A: Yes, you can. 1 1/2 is equivalent to 1.5. Half of 1.5 is 1.5 / 2 = 0.75, which is equivalent to 3/4.
Q: What if the question was "one-third of 1 1/2"?
A: You would follow a similar approach. First, convert 1 1/2 to an improper fraction (3/2). Then, multiply 3/2 by 1/3: (3/2) * (1/3) = 1/2.
Q: Why is converting to an improper fraction important?
A: Converting to an improper fraction simplifies the multiplication process. It allows you to perform the multiplication directly without needing to work with the whole number and fraction separately. It's a crucial skill in more advanced fraction manipulations.
Q: Are there any real-world applications of this concept?
A: Absolutely! Understanding fractions and mixed numbers is essential in various real-world scenarios, such as cooking (measuring ingredients), construction (measuring materials), and finance (calculating percentages).
Conclusion: More Than Just a Simple Calculation
While the question "half of 1 1/2" may seem simple at first glance, it serves as a valuable gateway to understanding fundamental mathematical concepts and problem-solving strategies. By exploring different approaches and emphasizing the underlying principles, we've moved beyond a simple calculation to a deeper appreciation of fractions, mixed numbers, and the elegance of mathematics. Mastering these fundamental concepts builds a strong foundation for more complex mathematical explorations in the future. The ability to approach problems from multiple angles and to translate abstract concepts into visual representations are critical skills that extend far beyond the realm of mathematics.
Latest Posts
Latest Posts
-
Animal Beginning With An N
Sep 25, 2025
-
What Time Does Church End
Sep 25, 2025
-
94 Degrees Fahrenheit In Celsius
Sep 25, 2025
-
Black Negative And Red Positive
Sep 25, 2025
-
Better In Person Dating App
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Half Of 1 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.