Integral Of 1 X 2
vittoremobilya
Sep 13, 2025 · 6 min read
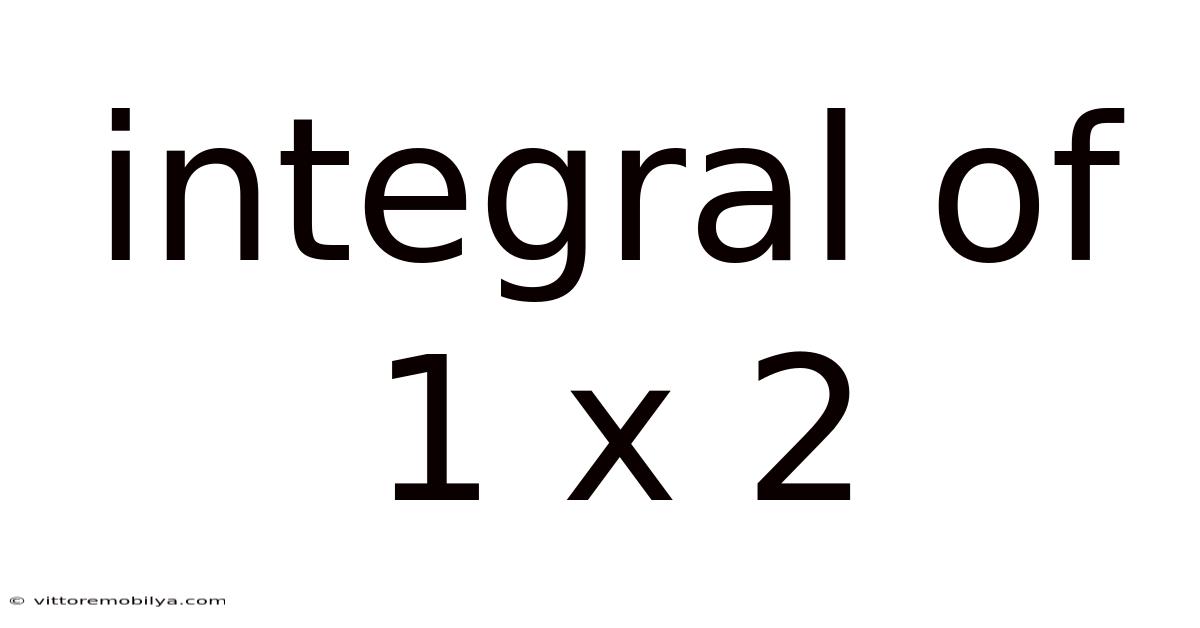
Table of Contents
Understanding and Solving the Integral of 1/x²: A Comprehensive Guide
The integral of 1/x², often written as ∫(1/x²)dx, is a fundamental concept in calculus. This article will provide a comprehensive explanation of how to solve this integral, covering various approaches and providing a deep understanding of the underlying principles. We'll delve into the power rule of integration, explore the connection to antiderivatives, and address potential misconceptions. By the end, you’ll not only be able to solve this specific integral but also possess a stronger foundation in integral calculus.
Introduction to Integration and the Power Rule
Integration is the reverse process of differentiation. While differentiation finds the instantaneous rate of change of a function, integration finds the area under the curve of a function. The integral of a function f(x) is denoted as ∫f(x)dx, where 'dx' indicates integration with respect to x. A crucial tool for solving many integrals is the power rule of integration. This rule states that the integral of x<sup>n</sup> is (x<sup>n+1</sup>)/(n+1) + C, where n is any real number except -1, and C is the constant of integration. This constant is essential because the derivative of a constant is always zero, meaning there are infinitely many functions that could have the same derivative.
Solving the Integral of 1/x² using the Power Rule
Let's rewrite 1/x² as x<sup>-2</sup>. Now, we can apply the power rule directly:
∫(1/x²)dx = ∫x<sup>-2</sup>dx
Using the power rule, where n = -2:
(x<sup>-2+1</sup>)/(-2+1) + C = (x<sup>-1</sup>)/(-1) + C = -x<sup>-1</sup> + C = -1/x + C
Therefore, the integral of 1/x² is -1/x + C, where C represents the constant of integration.
Visualizing the Integral: Area Under the Curve
It's helpful to visualize what this integral represents. The function 1/x² is a hyperbola. The definite integral of 1/x² between two points, say a and b (where a and b are not zero and a<b), represents the signed area under the curve of 1/x² from x = a to x = b. The 'signed' area means that areas below the x-axis are considered negative. The indefinite integral, -1/x + C, gives us a family of curves, each differing only by a vertical shift (determined by the constant C), whose derivative is 1/x².
Understanding the Constant of Integration (C)
The constant of integration, C, is a crucial aspect of indefinite integration. It represents the family of antiderivatives of the function. To illustrate, let's consider the derivatives of -1/x + 1, -1/x + 2, and -1/x + 3:
- d/dx (-1/x + 1) = 1/x²
- d/dx (-1/x + 2) = 1/x²
- d/dx (-1/x + 3) = 1/x²
All three functions have the same derivative, 1/x². The constant C accounts for this ambiguity. If we're dealing with a definite integral (an integral with specified limits of integration), the constant C cancels out during the evaluation process.
The Exception to the Power Rule: The Integral of 1/x
It's crucial to note that the power rule doesn't apply when n = -1. This is because the integral of 1/x is not x⁰/0, which is undefined. Instead, the integral of 1/x is ln|x| + C, where ln represents the natural logarithm. This integral is a common pitfall for students learning calculus. The absolute value signs are crucial because the natural logarithm is only defined for positive arguments.
Definite Integrals of 1/x²
Let's consider a definite integral:
∫<sub>1</sub><sup>2</sup> (1/x²) dx
Using the indefinite integral we derived earlier:
[-1/x]<sub>1</sub><sup>2</sup> = (-1/2) - (-1/1) = -1/2 + 1 = 1/2
This means the area under the curve of 1/x² from x = 1 to x = 2 is 1/2.
Applications of the Integral of 1/x²
The integral of 1/x² appears in numerous applications across various fields, including:
- Physics: Calculations involving inverse-square laws, like gravitational force or electrostatic force.
- Engineering: Solving differential equations that model various physical phenomena.
- Economics: Modeling certain aspects of economic growth and decay.
- Probability and Statistics: Involving probability density functions.
Common Mistakes and Misconceptions
Several common mistakes can occur when dealing with the integral of 1/x²:
- Forgetting the constant of integration (C): Always remember to include the constant of integration when solving indefinite integrals.
- Incorrectly applying the power rule when n = -1: Remember the special case of the integral of 1/x.
- Improper handling of negative exponents: Make sure to correctly handle negative exponents when applying the power rule.
Frequently Asked Questions (FAQ)
Q: What is the difference between a definite and an indefinite integral?
A: A definite integral has limits of integration (e.g., ∫<sub>a</sub><sup>b</sup> f(x) dx), resulting in a numerical value representing the area under the curve between those limits. An indefinite integral lacks limits of integration, resulting in a general antiderivative with a constant of integration (C).
Q: Why is the absolute value necessary in ln|x|?
A: The natural logarithm is only defined for positive arguments. The absolute value ensures that the argument of the natural logarithm is always positive, regardless of the sign of x.
Q: Can I use integration by parts or substitution to solve ∫(1/x²)dx?
A: While technically possible, it's not necessary or efficient. The power rule provides the most straightforward and efficient solution.
Q: What happens if I try to integrate 1/x² from -1 to 1?
A: The integral ∫<sub>-1</sub><sup>1</sup> (1/x²)dx is improper because the integrand is undefined at x = 0. This integral diverges (does not have a finite value). You would need to consider it as a sum of two improper integrals, one from -1 to 0 and another from 0 to 1. Each of these would diverge, leading to the divergence of the overall integral.
Conclusion
Understanding the integral of 1/x² is a cornerstone of calculus. By applying the power rule correctly and remembering the importance of the constant of integration, you can confidently solve this integral and many others. Understanding the underlying concepts, such as the connection between integration and differentiation, and the visual representation of the integral as an area under the curve, will enhance your comprehension and problem-solving skills in calculus. Remember to pay close attention to the special case of integrating 1/x and be wary of common mistakes to ensure accuracy in your calculations. With practice and a thorough understanding of these principles, you'll be well-equipped to tackle more complex integration problems.
Latest Posts
Latest Posts
-
Waist To Hip Ratio Calculator
Sep 13, 2025
-
Blessed Be Your Name Lyrics
Sep 13, 2025
-
How Long Do Tarantulas Live
Sep 13, 2025
-
God Give Me The Serenity
Sep 13, 2025
-
It Is Pleasure Meeting You
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.