Is 2/3 More Than 3/4
vittoremobilya
Sep 20, 2025 · 6 min read
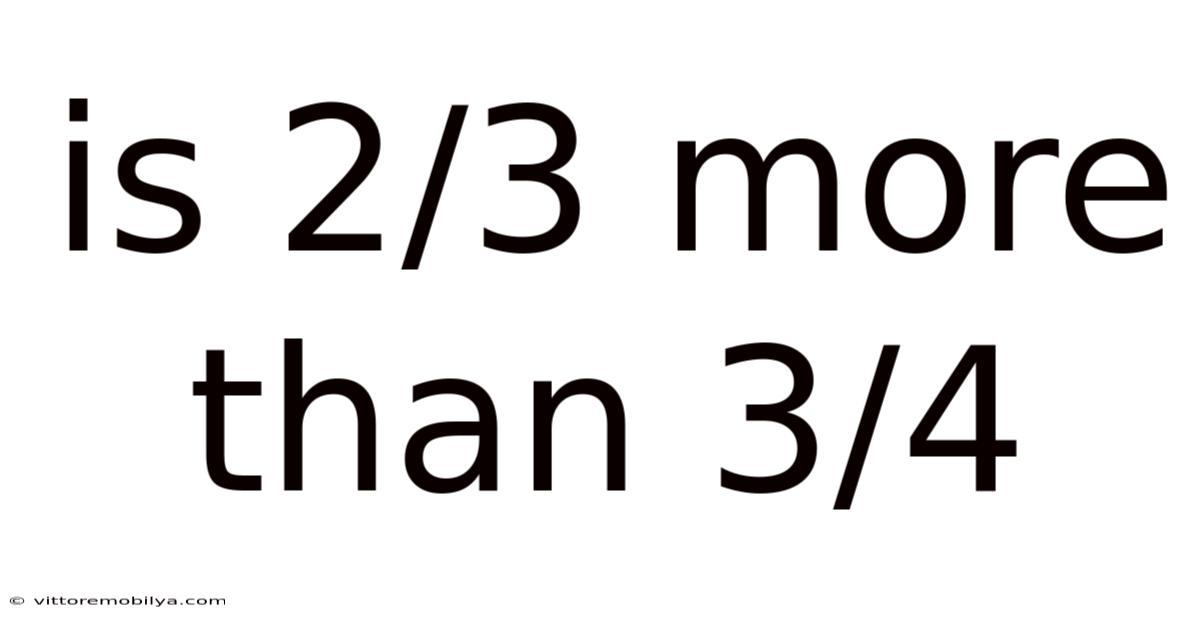
Table of Contents
Is 2/3 More Than 3/4? Understanding Fraction Comparison
This article will delve into the seemingly simple question: is 2/3 more than 3/4? While the answer might seem immediately obvious to some, understanding the why behind the answer is crucial for developing a strong foundation in fractions and mathematics in general. We'll explore various methods for comparing fractions, including visual representations, finding common denominators, converting to decimals, and even considering the concept of relative size. By the end, you'll not only know the answer but also possess a deeper understanding of fraction comparison techniques.
Introduction to Fraction Comparison
Fractions represent parts of a whole. Comparing fractions involves determining which fraction represents a larger portion of that whole. The question "Is 2/3 more than 3/4?" requires us to analyze and compare the relative sizes of these two fractions. This seemingly simple query opens the door to a wealth of mathematical concepts and problem-solving strategies. Mastering fraction comparison is fundamental to success in algebra, calculus, and numerous other mathematical disciplines.
Method 1: Visual Representation
One of the most intuitive ways to compare fractions is through visual aids. Imagine two identical circles. Divide the first circle into three equal parts and shade two of them, representing 2/3. Divide the second circle into four equal parts and shade three of them, representing 3/4. By visually comparing the shaded areas, it becomes readily apparent that 3/4 represents a larger portion of the whole than 2/3. This method is particularly helpful for beginners, providing a concrete understanding of fraction magnitude.
The visual representation reinforces the concept that fractions with larger numerators and smaller denominators generally indicate larger portions. While this visual method works well for simple fractions, it becomes less practical with more complex ones.
Method 2: Finding a Common Denominator
A more robust method involves finding a common denominator for both fractions. The denominator represents the total number of equal parts the whole is divided into. To compare 2/3 and 3/4, we need to find a common multiple of 3 and 4. The least common multiple (LCM) of 3 and 4 is 12.
-
Convert 2/3: To get a denominator of 12, we multiply both the numerator and denominator of 2/3 by 4: (2 * 4) / (3 * 4) = 8/12
-
Convert 3/4: To get a denominator of 12, we multiply both the numerator and denominator of 3/4 by 3: (3 * 3) / (4 * 3) = 9/12
Now we can easily compare 8/12 and 9/12. Since 9 > 8, we conclude that 9/12 (which is equivalent to 3/4) is greater than 8/12 (which is equivalent to 2/3). This method provides a precise and reliable way to compare any two fractions.
This method is particularly useful because it allows for direct numerical comparison, eliminating any ambiguity that might arise from visual representations. The concept of finding the LCM is a fundamental skill in various mathematical operations.
Method 3: Converting to Decimals
Another effective method is to convert both fractions to decimals. This involves dividing the numerator by the denominator for each fraction.
-
Convert 2/3: 2 ÷ 3 ≈ 0.6667
-
Convert 3/4: 3 ÷ 4 = 0.75
By comparing the decimal equivalents, 0.75 is clearly greater than 0.6667. Therefore, 3/4 is greater than 2/3. This method is straightforward and often preferred when dealing with calculations involving other decimal numbers.
The use of decimals introduces the concept of approximation, as some fractions, like 2/3, result in repeating decimals. However, for comparison purposes, a sufficient number of decimal places usually provides a clear result.
Method 4: Cross-Multiplication
A shortcut for comparing fractions is cross-multiplication. Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa. Compare the resulting products.
-
Cross-multiply 2/3 and 3/4:
- 2 * 4 = 8
- 3 * 3 = 9
Since 9 > 8, the fraction with the larger product (3/4) is the greater fraction. This method provides a quick and efficient way to compare fractions, particularly useful when dealing with larger numbers.
Cross-multiplication relies on the fundamental principle of equivalent fractions and provides a concise method for comparison, avoiding the need to find a common denominator directly.
Understanding Relative Size and Proportions
Beyond the mechanical processes of comparison, it's crucial to understand the relative size of fractions. While 3/4 is larger than 2/3, the difference isn't drastically large. Considering the context is essential. For example, if you're splitting a pizza, the difference between 2/3 and 3/4 of the pizza might not be significant. However, if you're dealing with larger quantities or percentages, the difference could be substantial. Understanding relative size enhances the application of fractions in real-world situations.
The concept of relative size also ties into proportions and ratios, which are fundamental in many areas, from cooking to engineering.
Illustrative Examples: Applying Fraction Comparison
Let's look at some practical examples demonstrating the application of these comparison methods:
-
Example 1: A baker has two cakes. One is 5/8 full, and the other is 2/3 full. Which cake has more left? Using the common denominator method (LCM of 8 and 3 is 24): 5/8 = 15/24 and 2/3 = 16/24. Therefore, the cake that is 2/3 full has more left.
-
Example 2: Two students scored 7/10 and 13/15 on a test. Who scored higher? Using cross-multiplication: 7 * 15 = 105 and 13 * 10 = 130. Therefore, the student who scored 13/15 scored higher.
-
Example 3: A recipe calls for 2/5 cup of sugar and 3/8 cup of flour. Is there more sugar or flour in the recipe? Using decimal conversion: 2/5 = 0.4 and 3/8 = 0.375. There is more sugar in the recipe.
Frequently Asked Questions (FAQ)
-
Q: Why is it important to learn how to compare fractions?
- A: Comparing fractions is a fundamental skill in mathematics, essential for higher-level math concepts and problem-solving across various fields. It enhances quantitative reasoning and problem-solving abilities.
-
Q: Which method is the "best" for comparing fractions?
- A: There's no single "best" method. The optimal approach depends on the complexity of the fractions and your personal preference. For simple fractions, visual representation or decimals might suffice. For more complex fractions, finding a common denominator or cross-multiplication is usually more efficient.
-
Q: What if I encounter fractions with very large numbers?
- A: For very large numbers, the common denominator method can become tedious. In such cases, converting to decimals or using a calculator to aid with cross-multiplication might be more efficient.
-
Q: Can I compare fractions with different signs (positive and negative)?
- A: Yes, when comparing fractions with different signs, a positive fraction will always be greater than a negative fraction. The magnitude of the fractions then determines which is larger within the positive or negative set separately.
Conclusion
The answer to "Is 2/3 more than 3/4?" is definitively no. 3/4 is greater than 2/3. However, the significance of this question lies not just in the answer itself but in the multiple methods and conceptual understandings it unlocks. Mastering fraction comparison is essential for building a strong mathematical foundation. Whether you use visual representations, common denominators, decimal conversions, or cross-multiplication, understanding the principles behind these methods empowers you to tackle more complex mathematical problems with confidence. The ability to compare fractions accurately extends far beyond simple arithmetic; it underpins your understanding of ratios, proportions, and many other mathematical concepts. Remember to choose the method that best suits your needs and the context of the problem, fostering a deeper appreciation for the versatility and practical application of fractions.
Latest Posts
Latest Posts
-
How Much Is 2 Tons
Sep 20, 2025
-
House Rental By Private Owner
Sep 20, 2025
-
How Much Is A Corgi
Sep 20, 2025
-
3 Things Hypnosis Cannot Do
Sep 20, 2025
-
Bill Cosby Net Worth 2024
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 More Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.