What Is 15 Of 90
vittoremobilya
Sep 13, 2025 · 6 min read
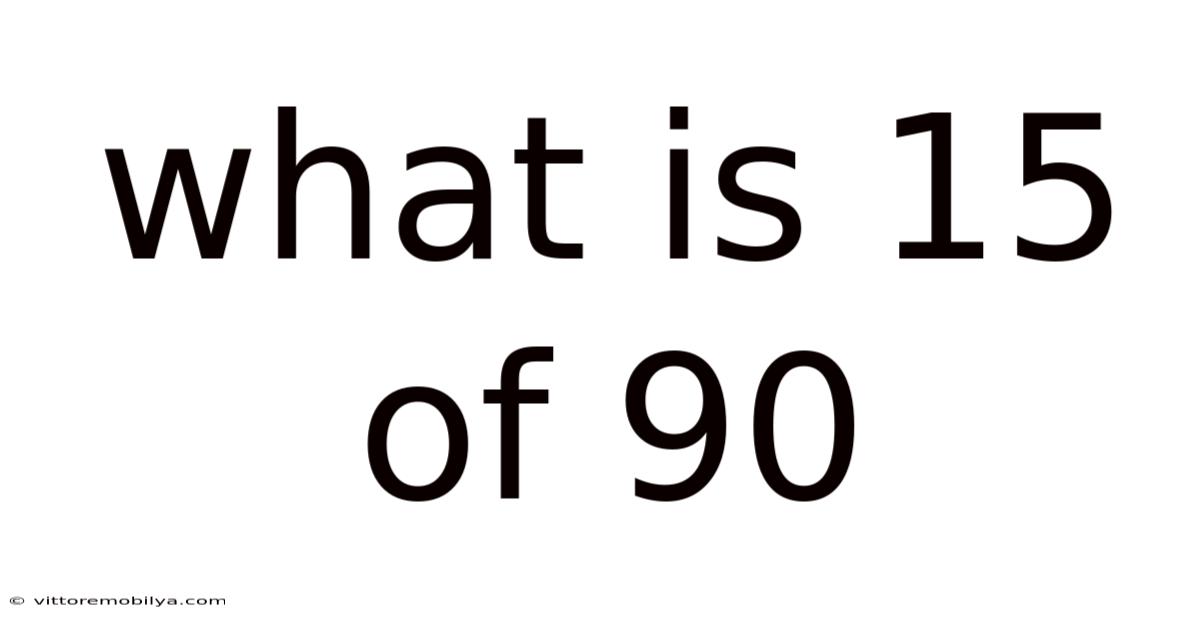
Table of Contents
What is 15/90? Unlocking the Power of Fractions and Percentages
Understanding fractions and percentages is a fundamental skill in mathematics, applicable across numerous fields from everyday budgeting to advanced scientific calculations. This article delves into the seemingly simple question, "What is 15/90?", but expands far beyond a mere numerical answer. We'll explore the different methods for solving this fraction, its equivalent percentage and decimal form, and the broader conceptual understanding of fractions and their real-world applications. This in-depth explanation will equip you with a solid foundation in working with fractions, allowing you to tackle more complex problems with confidence.
Understanding Fractions: A Foundation
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). In the fraction 15/90, 15 is the numerator, and 90 is the denominator. The fraction indicates that we have 15 parts out of a total of 90 equal parts.
Before we calculate 15/90, let's refresh some basic principles of fraction simplification:
- Common Factors: A crucial concept in simplifying fractions is identifying common factors between the numerator and denominator. A common factor is a number that divides both the numerator and denominator without leaving a remainder.
- Greatest Common Factor (GCF): The GCF is the largest number that divides both the numerator and the denominator evenly. Finding the GCF is essential for simplifying a fraction to its lowest terms.
- Simplifying Fractions: To simplify a fraction, we divide both the numerator and the denominator by their GCF. This results in an equivalent fraction that is easier to understand and work with.
Calculating 15/90: Step-by-Step
Now, let's determine the value of 15/90. We can solve this using a few different approaches:
Method 1: Direct Simplification using the GCF
The first and most efficient method involves finding the GCF of 15 and 90.
- List the factors of 15: 1, 3, 5, 15
- List the factors of 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
- Identify the GCF: The greatest common factor of 15 and 90 is 15.
Now, divide both the numerator and the denominator by the GCF (15):
15 ÷ 15 = 1 90 ÷ 15 = 6
Therefore, 15/90 simplifies to 1/6.
Method 2: Stepwise Simplification
If you don't immediately see the GCF, you can simplify the fraction step-by-step by dividing by any common factor you find. For instance:
- Divide both numerator and denominator by 5: 15/90 = 3/18
- Divide both numerator and denominator by 3: 3/18 = 1/6
This method achieves the same result (1/6) but might require more steps.
Method 3: Conversion to Decimal
Another approach is to convert the fraction to a decimal. To do this, divide the numerator (15) by the denominator (90):
15 ÷ 90 = 0.166666... (this is a repeating decimal)
This decimal, 0.16666..., is equivalent to 1/6.
Method 4: Using Percentage
To express 15/90 as a percentage, we can first simplify the fraction to 1/6 and then convert it:
1/6 = (1 ÷ 6) * 100% ≈ 16.67%
Therefore, 15/90 is approximately 16.67%. The percentage value is approximate because the decimal representation of 1/6 is a repeating decimal.
Real-World Applications of Fractions and Percentages
Understanding fractions and percentages is crucial for numerous aspects of daily life:
- Financial Literacy: Calculating discounts, interest rates, taxes, and budgeting all require working with fractions and percentages. For instance, understanding that a 20% discount means paying 80% of the original price is essential for smart shopping.
- Cooking and Baking: Recipes often use fractions to specify ingredient quantities, such as 1/2 cup of sugar or 2/3 cup of flour.
- Science and Engineering: Fractions and percentages are fundamental in many scientific calculations, including measurements, data analysis, and probability.
- Data Analysis and Statistics: Representing data proportions using fractions and percentages is essential for understanding trends and patterns. For example, a survey result might show that 15/90 respondents (or 16.67%) prefer a particular product.
- Probability and Statistics: In probability, fractions and percentages represent the likelihood of an event happening.
Understanding these mathematical concepts empowers you to make informed decisions and solve problems efficiently in various real-world situations.
Beyond the Basics: Further Exploration of Fractions
While this article focuses primarily on the calculation of 15/90, let's delve deeper into the broader world of fractions:
- Improper Fractions and Mixed Numbers: An improper fraction has a numerator greater than or equal to the denominator (e.g., 90/15). A mixed number combines a whole number and a fraction (e.g., 6). Improper fractions can be converted to mixed numbers and vice versa.
- Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. If they don't, you need to find a common denominator by finding the least common multiple (LCM) of the denominators.
- Multiplying and Dividing Fractions: Multiplying fractions involves multiplying the numerators and denominators separately. Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying.
Frequently Asked Questions (FAQs)
Q: Can I simplify a fraction by dividing the numerator and denominator by any number?
A: Yes, but only if the number divides both the numerator and denominator evenly (without leaving a remainder). The most efficient simplification uses the greatest common factor (GCF).
Q: What if I don't know how to find the GCF?
A: You can use a method called prime factorization. Break down both the numerator and denominator into their prime factors, then find the common factors and multiply them to find the GCF. For example:
15 = 3 x 5 90 = 2 x 3 x 3 x 5
The common factors are 3 and 5, so the GCF is 3 x 5 = 15.
Q: Are there any online calculators to help with fraction simplification?
A: Yes, many online calculators can simplify fractions. However, understanding the underlying principles is crucial for building a strong mathematical foundation.
Q: Why is it important to simplify fractions to their lowest terms?
A: Simplifying fractions makes them easier to understand and work with. It also provides a more concise and efficient representation of the quantity.
Conclusion: Mastering Fractions for a Brighter Future
In conclusion, 15/90 simplifies to 1/6, which is approximately 0.1667 or 16.67%. This seemingly simple calculation provides a springboard to understanding the fundamental concepts of fractions, percentages, and their extensive applications in various fields. By mastering these concepts, you equip yourself with a powerful toolset for problem-solving and decision-making across numerous aspects of life, from everyday tasks to complex professional endeavors. Remember, the journey to mathematical proficiency is a continuous process of learning, practicing, and applying your knowledge. Embrace the challenge, and the rewards will be substantial.
Latest Posts
Latest Posts
-
Air Jordan 4 Red Black
Sep 13, 2025
-
350 Small Block Firing Order
Sep 13, 2025
-
Gas Ratio For Weed Eater
Sep 13, 2025
-
How To Use A Steamer
Sep 13, 2025
-
Hand Over Heart National Anthem
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.