What Is 40 Of 2000
vittoremobilya
Sep 12, 2025 · 5 min read
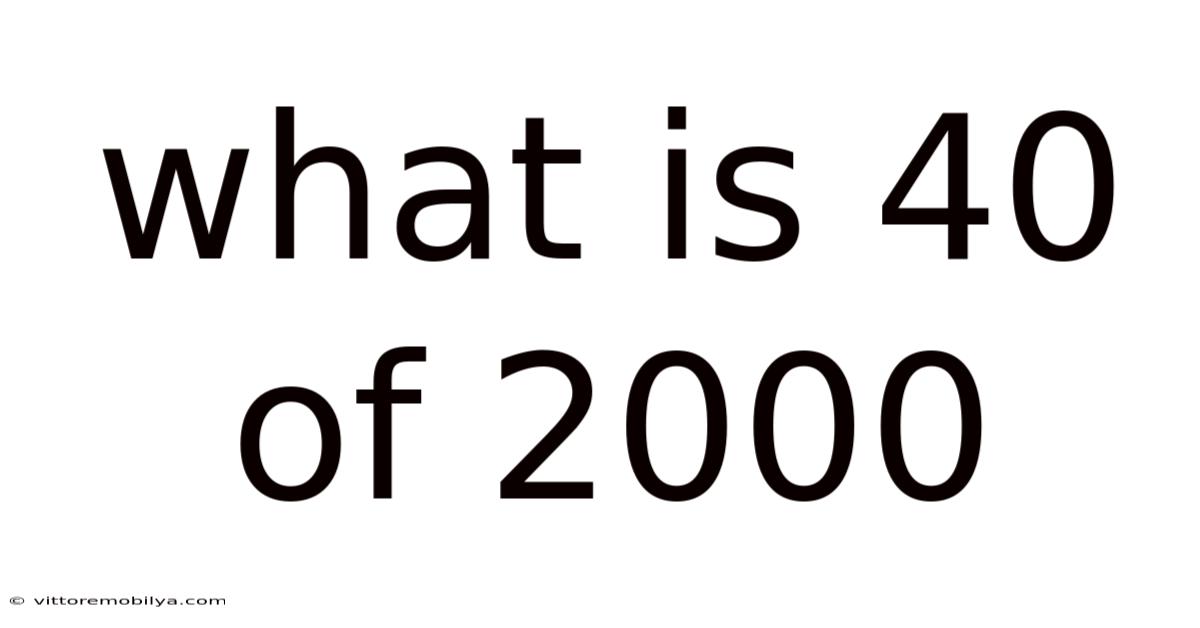
Table of Contents
What is 40% of 2000? A Comprehensive Guide to Percentages and Their Applications
Finding 40% of 2000 might seem like a simple arithmetic problem, but understanding the underlying concepts of percentages and their practical applications is crucial in various fields, from everyday finances to advanced statistical analysis. This article will not only provide the answer but also delve into the methods of calculating percentages, explore real-world examples, and address frequently asked questions, providing you with a comprehensive understanding of this fundamental mathematical concept.
Understanding Percentages: A Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." So, 40% literally means 40 out of 100, or 40/100. This can be simplified to the decimal 0.4. Understanding this fundamental relationship is key to calculating percentages effectively.
Method 1: Using Decimal Multiplication
This is arguably the most straightforward method for calculating percentages. We convert the percentage to a decimal and then multiply it by the given number.
Steps:
-
Convert the percentage to a decimal: To convert 40% to a decimal, divide it by 100: 40% / 100 = 0.4
-
Multiply the decimal by the number: Multiply the decimal (0.4) by the given number (2000): 0.4 * 2000 = 800
Therefore, 40% of 2000 is 800.
Method 2: Using Fractions
This method involves converting the percentage to a fraction and then multiplying it by the given number.
Steps:
-
Convert the percentage to a fraction: 40% can be written as the fraction 40/100.
-
Simplify the fraction (if possible): The fraction 40/100 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 20. This simplifies to 2/5.
-
Multiply the fraction by the number: Multiply the simplified fraction (2/5) by the given number (2000): (2/5) * 2000 = 800
Again, we arrive at the answer: 40% of 2000 is 800.
Method 3: Using Proportions
This method involves setting up a proportion to solve for the unknown value.
Steps:
-
Set up a proportion: We can set up a proportion as follows: x/2000 = 40/100, where 'x' represents 40% of 2000.
-
Cross-multiply: Cross-multiplying gives us 100x = 80000.
-
Solve for x: Divide both sides by 100 to solve for x: x = 800
Once again, the result is: 40% of 2000 is 800.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in various real-world scenarios:
-
Finance: Calculating interest on loans, savings accounts, and investments. For example, calculating the interest earned on a savings account with an annual interest rate of 4% on a balance of $2000.
-
Sales and Discounts: Determining the final price after applying a discount percentage. Imagine a $2000 item is on sale with a 40% discount. The discount amount is 40% of $2000, which is $800, resulting in a final price of $1200.
-
Statistics and Data Analysis: Expressing proportions and changes in data as percentages. This could involve calculating the percentage increase or decrease in sales, population, or any other measurable quantity. For example, if a company's sales increased from 1000 units to 2000 units, the percentage increase is 100%.
-
Tax Calculations: Determining the amount of tax owed on income, purchases, or property. If the sales tax rate is 4%, then the tax on a $2000 item would be 4% of $2000, which is $80.
-
Grade Calculations: Many academic systems utilize percentages to represent grades, making understanding percentage calculations essential for students to track their academic progress.
-
Surveys and Polls: Results of surveys and polls are often presented as percentages to represent the proportion of respondents who chose a specific option.
Beyond the Basics: Understanding Percentage Change
Often, we need to calculate the percentage change between two numbers. This involves finding the difference between the two numbers, dividing that difference by the original number, and then multiplying by 100 to express the result as a percentage.
Formula for Percentage Change: [(New Value - Old Value) / Old Value] * 100
For example, if the price of an item increased from $1000 to $2000, the percentage change would be: [(2000 - 1000) / 1000] * 100 = 100%, representing a 100% increase.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a different percentage of 2000?
A1: Follow the same methods outlined above, simply substituting the desired percentage for 40%. For instance, to find 25% of 2000, you would convert 25% to 0.25 and multiply it by 2000 (0.25 * 2000 = 500).
Q2: What if I need to find what percentage one number is of another?
A2: To find what percentage one number is of another, divide the first number by the second number, and then multiply by 100. For example, to find what percentage 800 is of 2000, you would divide 800 by 2000 (800/2000 = 0.4), and then multiply by 100 (0.4 * 100 = 40%). Therefore, 800 is 40% of 2000.
Q3: Are there any online calculators available to help with percentage calculations?
A3: Yes, many free online percentage calculators are available. These calculators can simplify the process, especially for more complex calculations. However, understanding the underlying principles remains crucial for solving problems effectively and independently.
Q4: What are some common mistakes to avoid when calculating percentages?
A4: Common mistakes include incorrectly converting percentages to decimals, forgetting to multiply by 100 when expressing the result as a percentage, and confusing the order of operations when dealing with multiple calculations. Careful attention to detail and a systematic approach are key to avoiding these errors.
Conclusion: Mastering the Power of Percentages
Calculating 40% of 2000, resulting in 800, is just one example of the broader application of percentages. This seemingly simple calculation underlies numerous critical processes in various aspects of life. By understanding the different methods for calculating percentages and their practical applications, you equip yourself with a powerful tool for navigating the quantitative world, from managing your finances to understanding data-driven decisions. Remember to practice consistently to build fluency and accuracy in your calculations. The more you practice, the more comfortable and confident you will become in using percentages effectively.
Latest Posts
Latest Posts
-
Wire Black With White Stripe
Sep 12, 2025
-
How Does A Creampie Feel
Sep 12, 2025
-
License Plate With Red Letters
Sep 12, 2025
-
What Is 6 In Inches
Sep 12, 2025
-
How To Break A Sissy
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 2000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.