X 2 5 X 2
vittoremobilya
Sep 24, 2025 · 6 min read
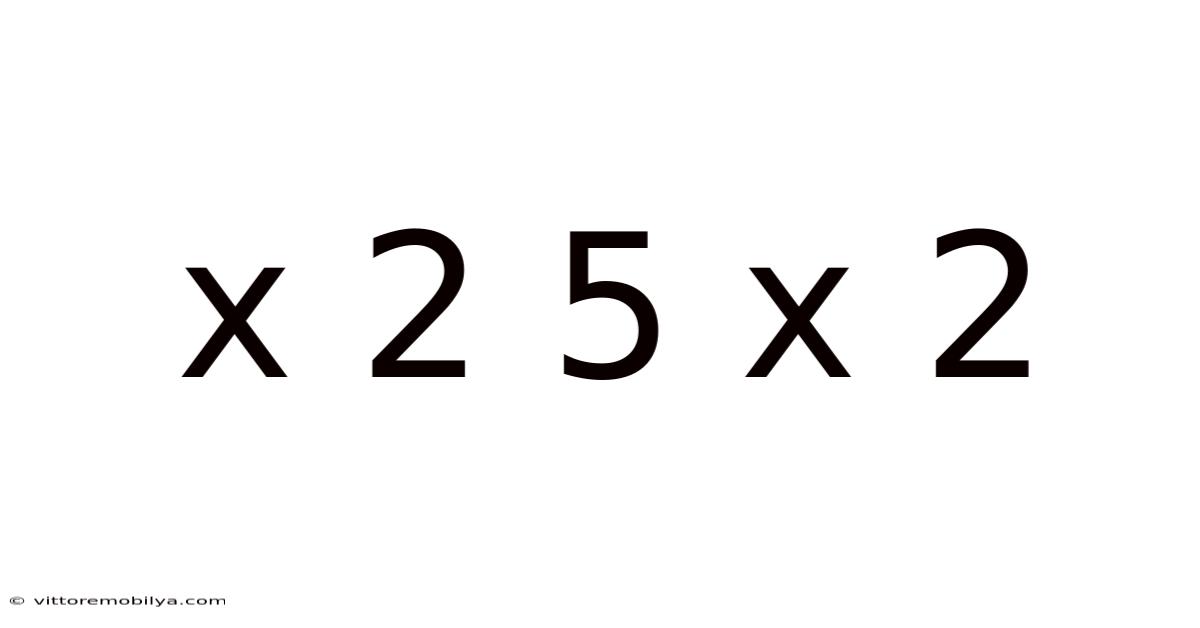
Table of Contents
Decoding X² + 5X + 2: A Comprehensive Exploration of Quadratic Equations
This article delves into the intricacies of the quadratic expression x² + 5x + 2, exploring its various facets from basic understanding to advanced applications. We'll cover solving for x, graphing the parabola, understanding its discriminant, and even touching on real-world applications of such equations. This comprehensive guide is designed for anyone from high school students encountering quadratic equations for the first time to those seeking a refresher on the topic. Whether you're struggling with factoring, using the quadratic formula, or visualizing the graph, this article aims to illuminate the subject and build your confidence in handling quadratic expressions.
Understanding Quadratic Equations: A Quick Overview
Before diving into the specifics of x² + 5x + 2, let's establish a foundational understanding of quadratic equations. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually x) is 2. The general form of a quadratic equation is ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero (otherwise, it wouldn't be a quadratic equation). Our focus, x² + 5x + 2, is a quadratic expression, meaning it's not yet set equal to zero, but it can easily be turned into an equation by setting it equal to a value (often zero).
Solving for x: Factoring, Quadratic Formula, and Completing the Square
Solving a quadratic equation means finding the values of x that satisfy the equation. There are several methods for doing this:
1. Factoring:
Factoring involves expressing the quadratic expression as a product of two linear expressions. This method is the most straightforward but only works for certain quadratic equations. Unfortunately, x² + 5x + 2 cannot be easily factored using integers. There are no two integers that add up to 5 and multiply to 2. This leads us to other methods.
2. Quadratic Formula:
The quadratic formula is a powerful tool that works for all quadratic equations, regardless of whether they can be factored easily. The formula is derived from completing the square method and is given by:
x = (-b ± √(b² - 4ac)) / 2a
For our equation, x² + 5x + 2 = 0, we have a = 1, b = 5, and c = 2. Substituting these values into the quadratic formula gives us:
x = (-5 ± √(5² - 4 * 1 * 2)) / (2 * 1) x = (-5 ± √(25 - 8)) / 2 x = (-5 ± √17) / 2
Therefore, the two solutions for x are:
x₁ = (-5 + √17) / 2 ≈ -0.438 x₂ = (-5 - √17) / 2 ≈ -4.562
These are the exact solutions. Approximations are provided for practical understanding.
3. Completing the Square:
Completing the square is another method for solving quadratic equations. It involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. While the quadratic formula is often quicker, completing the square is a valuable technique for understanding the underlying structure of quadratic equations and has applications beyond solving equations directly. Applying this method to x² + 5x + 2 requires several steps involving algebraic manipulation and is best illustrated step-by-step in a dedicated tutorial; however, it will ultimately lead to the same solutions as the quadratic formula.
Graphing the Parabola: Visualizing the Quadratic Equation
The graph of a quadratic equation is a parabola, a U-shaped curve. Understanding the parabola's characteristics helps visualize the solutions (roots) of the equation. The vertex of the parabola represents the minimum or maximum point of the curve. The x-intercepts, where the parabola crosses the x-axis, correspond to the solutions (roots) we found using the quadratic formula.
For x² + 5x + 2, the parabola opens upwards (since the coefficient of x² is positive). The x-intercepts are approximately -0.438 and -4.562, as calculated previously. The vertex's x-coordinate can be found using the formula -b/2a = -5/(2*1) = -2.5. Substituting this value back into the equation gives the y-coordinate of the vertex. Therefore, the vertex is approximately at (-2.5, -4.25). This information allows us to accurately sketch the parabola, providing a visual representation of the equation's behavior.
The Discriminant: Unveiling the Nature of the Roots
The discriminant (b² - 4ac) within the quadratic formula plays a crucial role in determining the nature of the roots (solutions) of the quadratic equation.
- If b² - 4ac > 0: The equation has two distinct real roots. This is the case for x² + 5x + 2, as the discriminant (17) is positive.
- If b² - 4ac = 0: The equation has exactly one real root (a repeated root).
- If b² - 4ac < 0: The equation has no real roots; the roots are complex conjugates (involving imaginary numbers).
For x² + 5x + 2, the discriminant is 17, which is positive. This confirms that the equation has two distinct real roots, as we already found using the quadratic formula.
Applications of Quadratic Equations in Real Life
Quadratic equations are not merely abstract mathematical concepts; they have numerous real-world applications across various fields:
- Physics: Projectile motion (e.g., calculating the trajectory of a ball thrown into the air) is often modeled using quadratic equations.
- Engineering: Designing structures, bridges, and other engineering marvels often involves solving quadratic equations to ensure stability and efficiency.
- Economics: Analyzing economic growth and decay, determining optimal pricing strategies, and modeling supply and demand curves may utilize quadratic equations.
- Computer Graphics: Creating curves and shapes in computer graphics and animation often employs quadratic functions.
Frequently Asked Questions (FAQ)
Q: Can all quadratic equations be solved by factoring?
A: No. While factoring is a convenient method for some quadratic equations, many cannot be factored easily using integers. The quadratic formula provides a universal method for solving all quadratic equations.
Q: What does the vertex of a parabola represent?
A: The vertex of a parabola represents the minimum (if the parabola opens upwards) or maximum (if the parabola opens downwards) point of the curve. It's a crucial point for understanding the overall behavior of the quadratic function.
Q: What is the significance of the discriminant?
A: The discriminant helps determine the nature and number of roots (solutions) of a quadratic equation. A positive discriminant indicates two distinct real roots, a zero discriminant indicates one repeated real root, and a negative discriminant indicates no real roots (complex roots).
Q: Can a quadratic equation have only one solution?
A: Yes. This occurs when the discriminant is equal to zero, resulting in a repeated root. The parabola touches the x-axis at only one point.
Q: Are there other methods to solve quadratic equations besides factoring, the quadratic formula, and completing the square?
A: Yes, numerical methods like the Newton-Raphson method can be used to approximate the solutions of quadratic equations, especially when dealing with more complex equations that are difficult to solve analytically. However, the methods discussed above are the most fundamental and widely used.
Conclusion
The quadratic expression x² + 5x + 2, though seemingly simple, embodies the core concepts of quadratic equations. By understanding how to solve for x, visualize the parabola, and interpret the discriminant, we unlock a powerful tool applicable across numerous fields. This comprehensive exploration provides a robust foundation for further studies in algebra and its practical applications. Remember, mastering quadratic equations is a stepping stone to tackling more complex mathematical challenges. Consistent practice and a willingness to explore different solution methods will solidify your understanding and boost your confidence in tackling any quadratic expression you encounter.
Latest Posts
Latest Posts
-
How To Get Vapes Underage
Sep 24, 2025
-
Can Stomach Acid Dissolve Plastic
Sep 24, 2025
-
You Make Stray Kids Stay
Sep 24, 2025
-
Teach Them To Fish Bible
Sep 24, 2025
-
What Is 1 2 Teaspoon
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about X 2 5 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.