X2 5x 6 X 2
vittoremobilya
Sep 18, 2025 · 6 min read
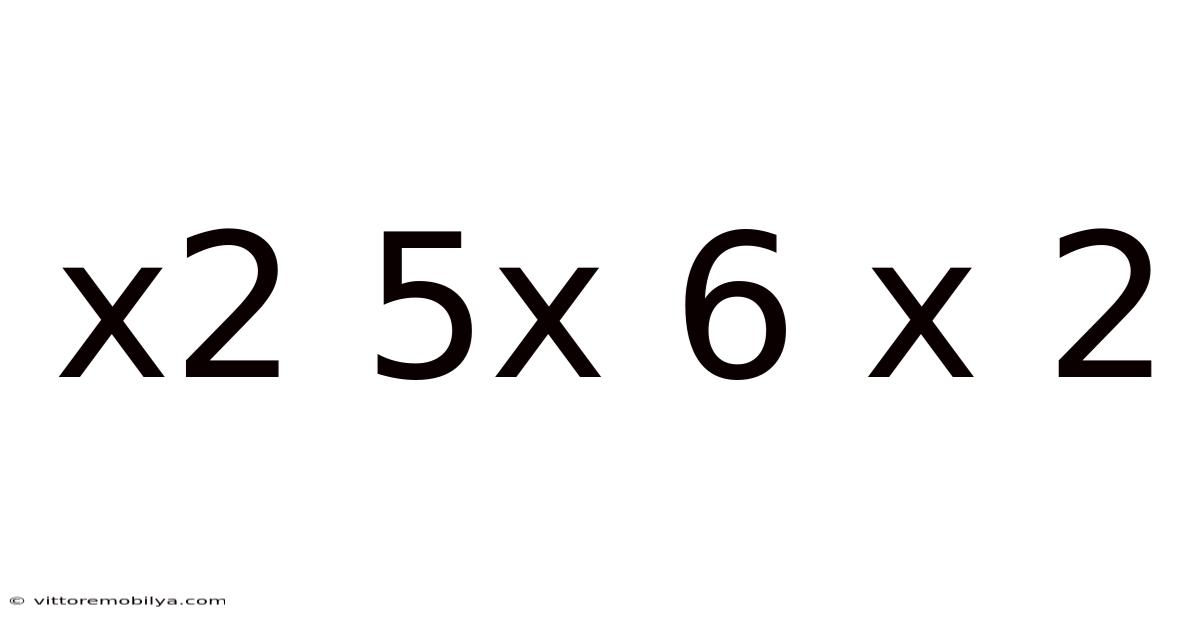
Table of Contents
Decoding the Mathematical Expression: x² + 5x + 6 = 0
This article delves into the complete analysis of the quadratic equation x² + 5x + 6 = 0. We'll explore various methods for solving this equation, understand the underlying mathematical concepts, and examine the significance of its solutions within a broader mathematical context. This exploration will be suitable for anyone from high school students beginning their journey with algebra to those looking for a refresher on fundamental mathematical principles. We will cover everything from factoring to the quadratic formula, and even touch upon the graphical representation of this equation.
Introduction: Understanding Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (in this case, 'x') is 2. The general form of a quadratic equation is ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our specific equation, x² + 5x + 6 = 0, fits this form with a = 1, b = 5, and c = 6. Understanding quadratic equations is crucial in various fields, including physics, engineering, and economics, where they model many real-world phenomena.
Method 1: Factoring the Quadratic Expression
Factoring is a powerful technique for solving quadratic equations. It involves expressing the quadratic expression as a product of two linear expressions. The goal is to find two numbers that add up to 'b' (in our case, 5) and multiply to 'c' (in our case, 6).
Let's find those numbers: The numbers 2 and 3 satisfy these conditions because 2 + 3 = 5 and 2 * 3 = 6. Therefore, we can factor the quadratic expression as follows:
x² + 5x + 6 = (x + 2)(x + 3) = 0
Now, we can solve for x by setting each factor equal to zero:
- x + 2 = 0 => x = -2
- x + 3 = 0 => x = -3
Therefore, the solutions to the equation x² + 5x + 6 = 0 are x = -2 and x = -3. These are also known as the roots or zeros of the quadratic equation.
Method 2: Using the Quadratic Formula
The quadratic formula provides a general solution for any quadratic equation of the form ax² + bx + c = 0. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Let's apply this formula to our equation, where a = 1, b = 5, and c = 6:
x = [-5 ± √(5² - 4 * 1 * 6)] / (2 * 1) x = [-5 ± √(25 - 24)] / 2 x = [-5 ± √1] / 2 x = [-5 ± 1] / 2
This gives us two solutions:
- x = (-5 + 1) / 2 = -4 / 2 = -2
- x = (-5 - 1) / 2 = -6 / 2 = -3
As expected, we obtain the same solutions as with the factoring method: x = -2 and x = -3. The quadratic formula is particularly useful when factoring is difficult or impossible.
Method 3: Completing the Square
Completing the square is another algebraic technique to solve quadratic equations. It involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
Here's how to complete the square for x² + 5x + 6 = 0:
-
Move the constant term to the right side: x² + 5x = -6
-
Take half of the coefficient of x (which is 5), square it ( (5/2)² = 6.25 ), and add it to both sides: x² + 5x + 6.25 = -6 + 6.25 x² + 5x + 6.25 = 0.25
-
Factor the left side as a perfect square: (x + 2.5)² = 0.25
-
Take the square root of both sides: x + 2.5 = ±√0.25 = ±0.5
-
Solve for x: x = -2.5 ± 0.5
This gives us the solutions:
- x = -2.5 + 0.5 = -2
- x = -2.5 - 0.5 = -3
Again, we arrive at the same solutions: x = -2 and x = -3. Completing the square is a valuable technique that is often used in other areas of mathematics, such as conic sections.
Graphical Representation
The quadratic equation x² + 5x + 6 = 0 can be represented graphically as a parabola. The x-intercepts of the parabola represent the solutions to the equation. The parabola opens upwards because the coefficient of x² (which is 1) is positive. The vertex of the parabola, which represents the minimum point, lies at x = -2.5 and y = -0.25. The x-intercepts, where the parabola crosses the x-axis, are at x = -2 and x = -3, confirming our solutions.
The Discriminant and Nature of Roots
The expression b² - 4ac within the quadratic formula is called the discriminant. The discriminant determines the nature of the roots of the quadratic equation:
- If b² - 4ac > 0: The equation has two distinct real roots (as in our case).
- If b² - 4ac = 0: The equation has one real root (a repeated root).
- If b² - 4ac < 0: The equation has two complex roots (involving imaginary numbers).
In our equation, the discriminant is 5² - 4 * 1 * 6 = 1, which is greater than 0, indicating two distinct real roots, as we've already found.
Applications of Quadratic Equations
Quadratic equations have a wide range of applications across various disciplines. Here are a few examples:
- Physics: Calculating the trajectory of a projectile, determining the velocity of an object under constant acceleration.
- Engineering: Designing structures, analyzing electrical circuits, modelling vibrations.
- Economics: Analyzing market equilibrium, maximizing profits, calculating optimal production levels.
- Computer graphics: Creating curves and shapes, modelling 3D objects.
Frequently Asked Questions (FAQ)
Q: What does it mean to "solve" a quadratic equation?
A: Solving a quadratic equation means finding the values of the variable (x) that make the equation true. These values are called the roots or solutions of the equation.
Q: Can a quadratic equation have more than two solutions?
A: No, a quadratic equation can have at most two solutions. This is because the highest power of the variable is 2.
Q: What if I can't factor the quadratic expression easily?
A: If factoring is difficult, you can always use the quadratic formula to find the solutions.
Q: What is the significance of the discriminant?
A: The discriminant tells you the nature of the roots (real or complex, distinct or repeated) without actually solving the equation.
Conclusion
The equation x² + 5x + 6 = 0, seemingly simple, provides a rich opportunity to explore fundamental concepts in algebra. We’ve explored three different methods – factoring, the quadratic formula, and completing the square – all leading to the same solutions: x = -2 and x = -3. Understanding these methods and the underlying principles is essential for tackling more complex mathematical problems. The graphical representation helps visualize the solutions and provides an intuitive understanding of the equation's behavior. The concept of the discriminant further enhances our understanding of the nature of the roots. This comprehensive exploration showcases the power and elegance of quadratic equations and their significance in various fields. The exploration of this seemingly simple equation lays the groundwork for understanding more intricate mathematical concepts encountered in higher-level mathematics and related disciplines.
Latest Posts
Latest Posts
-
How To Have A Threesome
Sep 18, 2025
-
Yo Momma So Fat Jokes
Sep 18, 2025
-
Things To Say During Sex
Sep 18, 2025
-
Freemasonry And The Holy Bible
Sep 18, 2025
-
Dry Cleaning Prices Near Me
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about X2 5x 6 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.